A planet of mass , has two natural satellites with masses and . The radii of their circular orbits are and respectively. Ignore the gravitational force between the satellites. Define , and to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1, and , , and to be the corresponding quantities of satellite 2. Given/2and/1/4, match the ratios in List-I to the numbers in List-II.
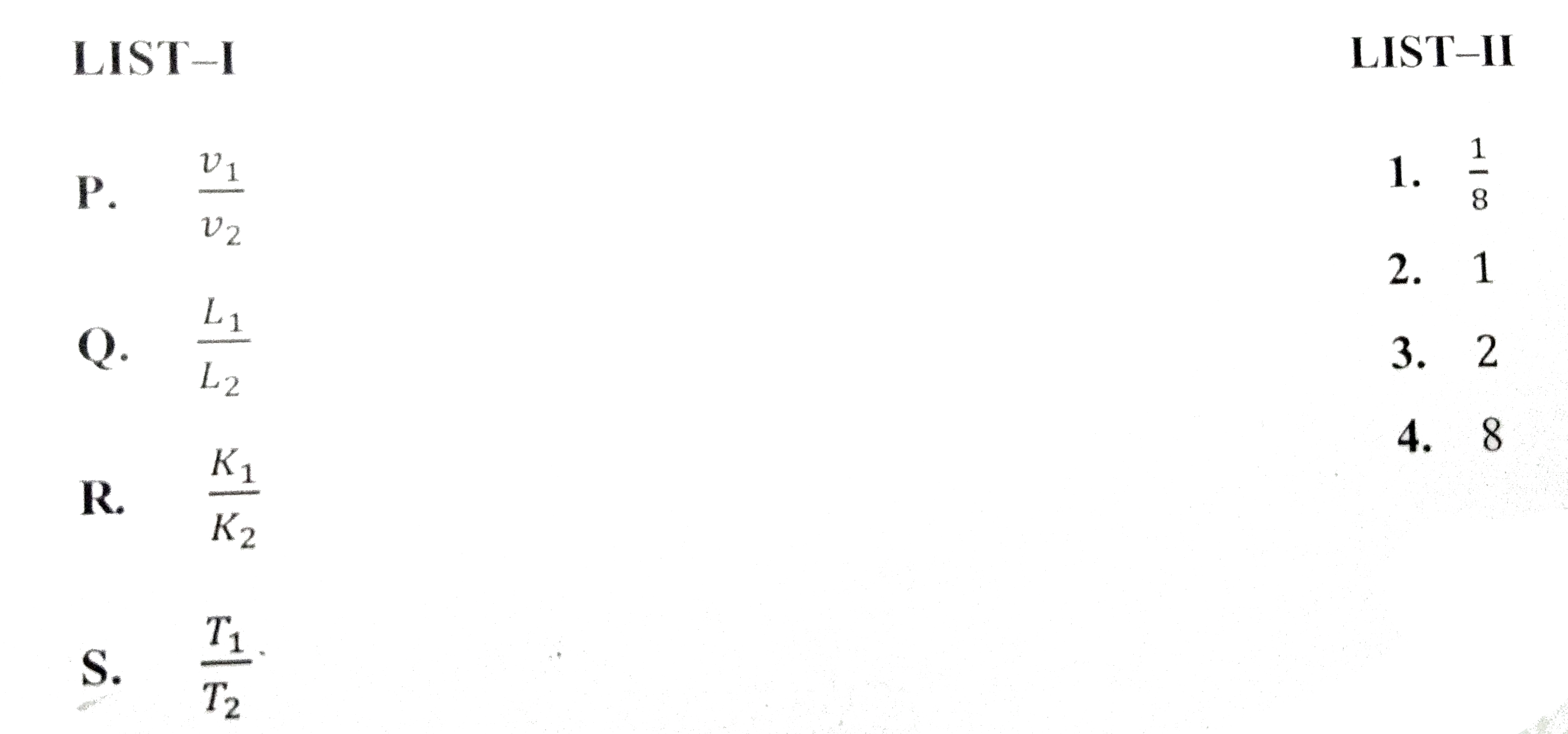
P→4,Q→2,R→1,S→3
P→3,Q→2,R→4,S→1
P→2,Q→3,R→1,S→4
P→2,Q→3,R→4,S→1
The correct Answer is:B
Step by step video, text & image solution for A planet of mass , has two natural satellites with masses and . The radii of their circular orbits are and respectively. Ignore the gravitational force between the satellites. Define , and to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1, and , , and to be the corresponding quantities of satellite 2. Given//2 and //1//4, match the ratios in List-I to the numbers in List-II. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXERCISE-3 PART-211videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXERCISE-2 PART-49videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions16videos
NUCLEAR PHYSICS
Similar Questions
A planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
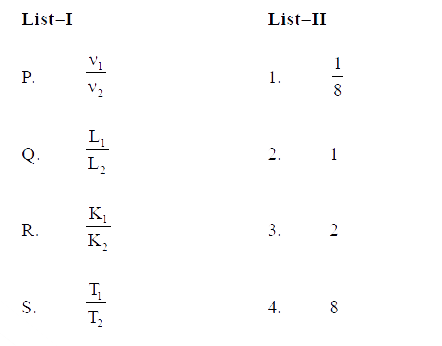 View Solution
View SolutionIf gravitational forces between a planet and a satellite is proportional to R−5/2. If R is the orbit radius. Then the period of revolution of satellites is proportional to Rn. Find n.
View Solution
Knowledge Check
- Question 1 - Select One
Two satellites of masses 3 m and m orbit the earth in circular orbits of radii r and 3 r respectively. The ratio of the their speeds is
A1:1B√3:1C3:1D9:1 - Question 2 - Select One
Two satellite fo masses m and 4m orbit the earth in circular orbits of radii 4r and r respectively. The ratio of their orbital speed is
A1B12C1√2D1√5 - Question 3 - Select One
Two satellites of same mass are launched in circular orbits at height of 2R and 3R respectively. The ration of kinetic energies is
A2:3B1:1C3:2D1:3
A satellite of the earth is revolving in a circular orbit with a uniform speed v. If the gravitational force suddenly disappears, the satellite will
View SolutionA satellite of the earth is revolving in circular orbit with a uniform velocity V. If the gravitational force suddenly disappers, the satellite will-
View SolutionA satellite of the earth is revolving in a circular orbit with a uniform speed v. If gravitational force suddenly disappears, the satellite will
View SolutionA satellite is revolving around earth in a circular orbit at a uniform speed v . If gravitational force suddenly disappears , speed of the satellite will be
View SolutionTwo satellites of masses M and 4M are orbiting the earth in a circular orbit of radius r. Their frequencies of revolution are in the ratio of
View Solution

