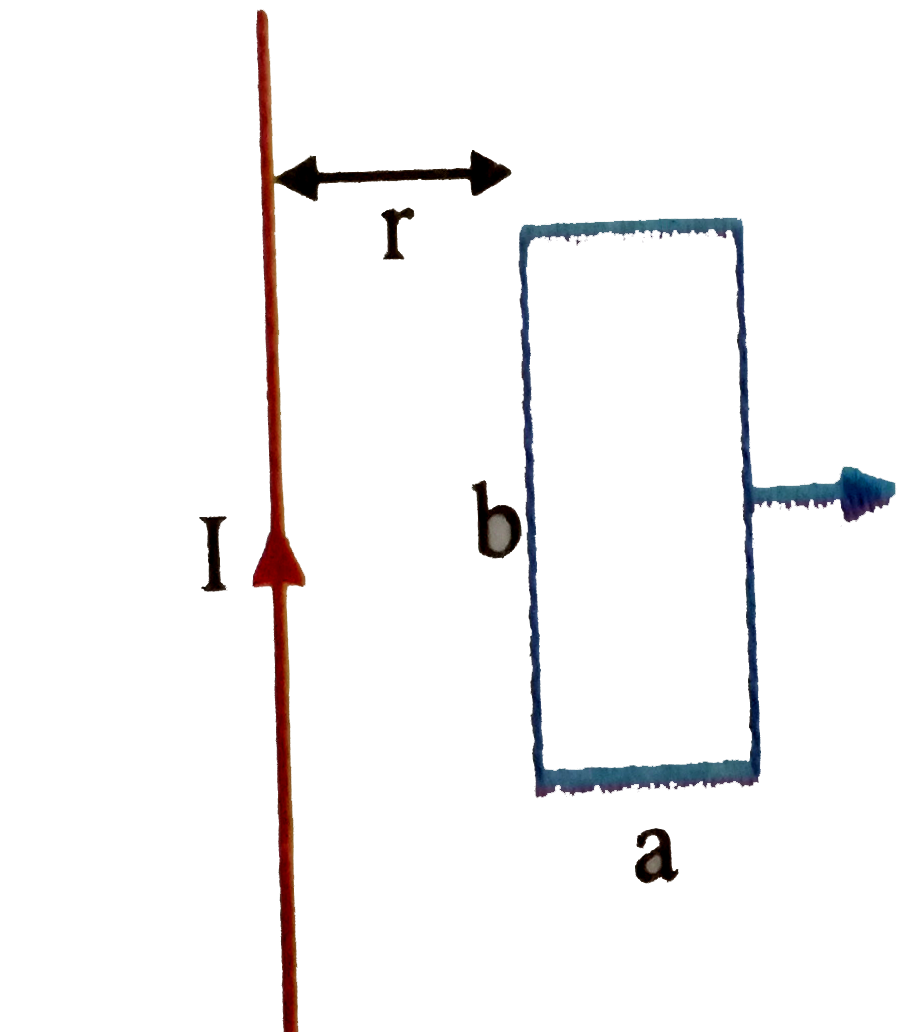
a rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
E=B1LV−B2Lv=μ0i2πxLv−μ0i2π(x+b)Lv=μ0iLbv2πx(x+b)
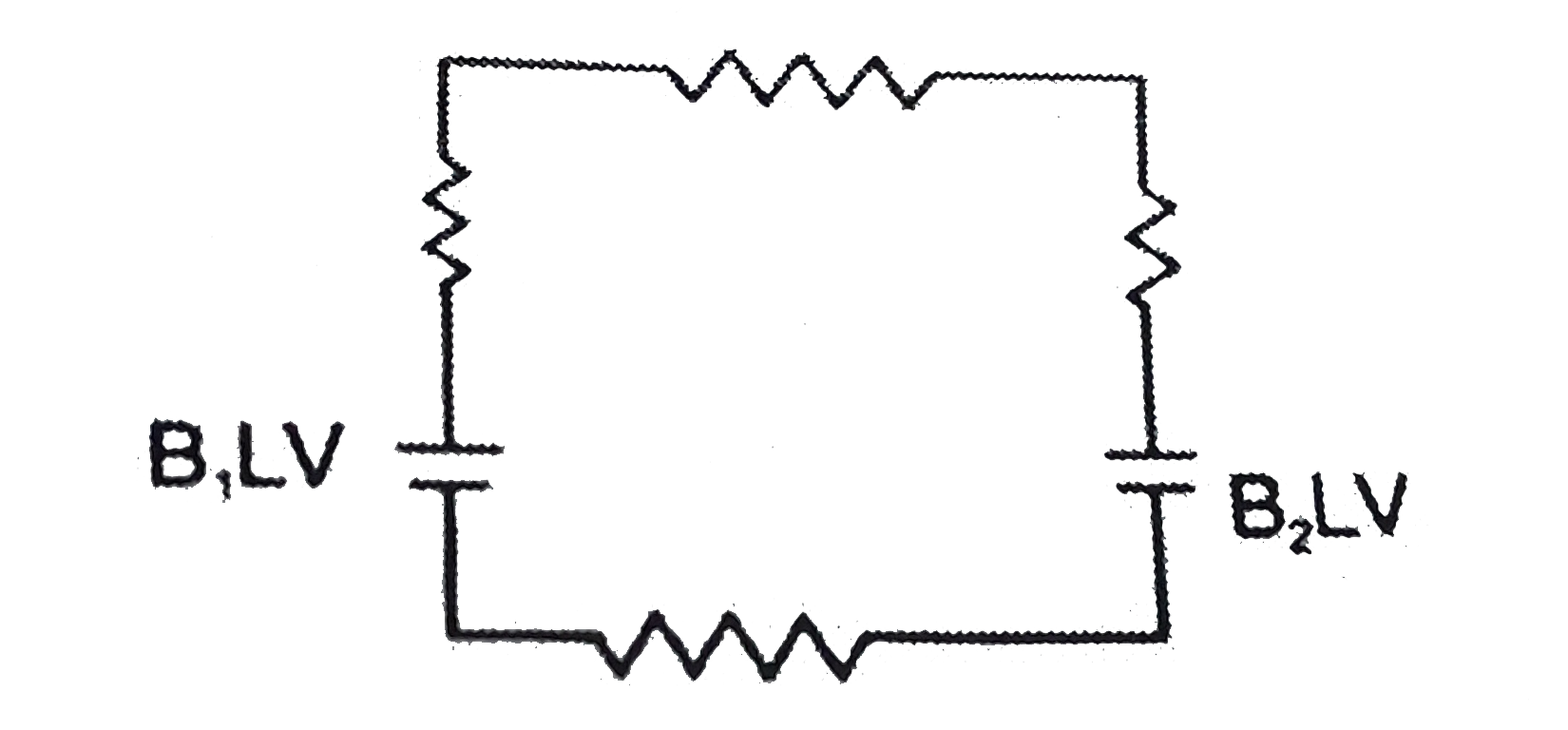
Alter:
Consider a small segment of width dy at a distance y from the wire.
Let flux through the segment be dϕ.
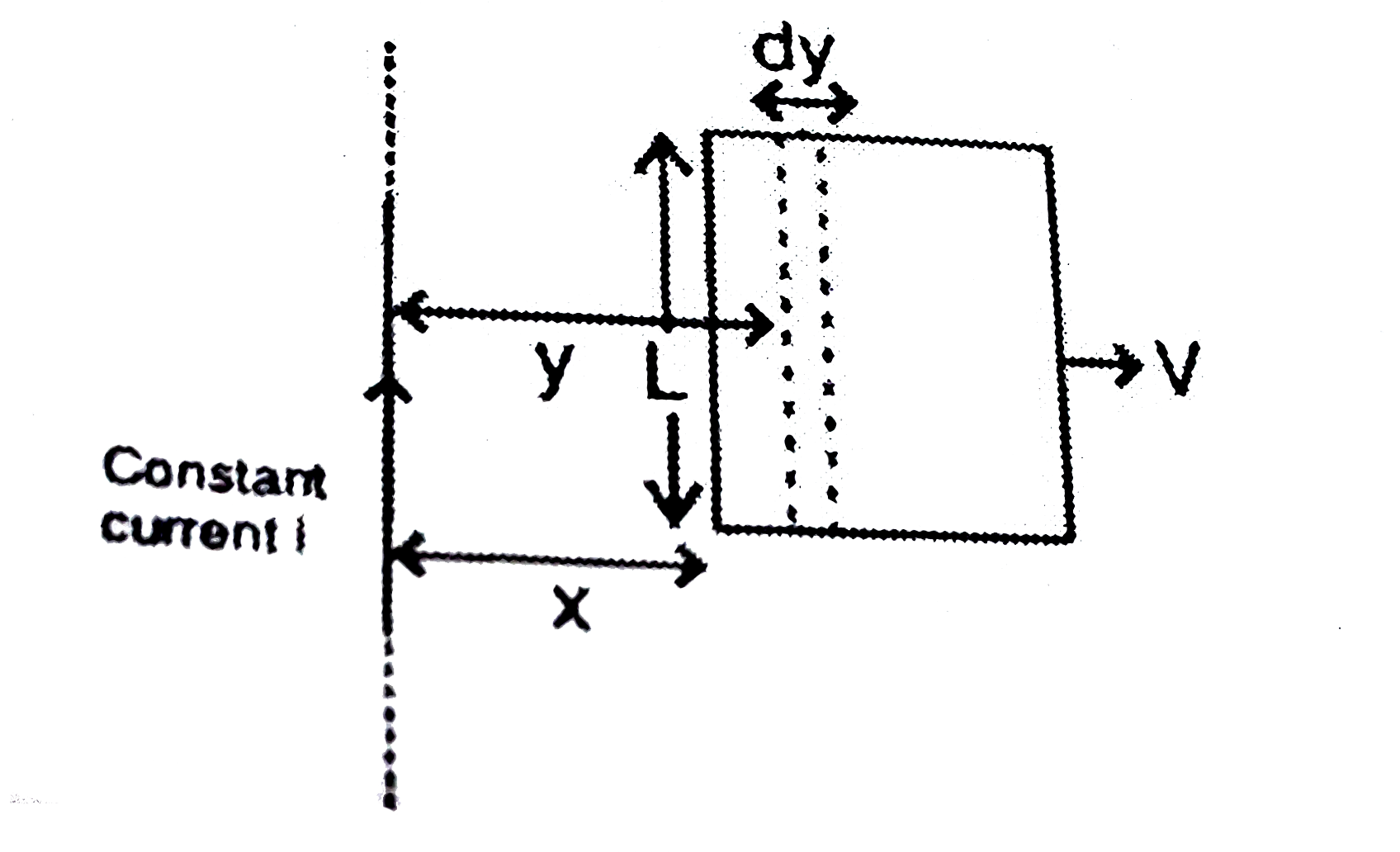
∴dϕ=μ0i2πyLdy ∴ϕ=μ0iL2π∫x+bxdyy=μ0iL2π(ln(x+b)−lnx)
Now dϕdt=μ0iL2π[1x+bdxdt−1xdxdt]v=−μ0ibLv2πx(x+b)
∴ induced emf =μ0ibLv2πx(x+b)
Similar Questions
A rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.
View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.
View Solution
Knowledge Check
A rectangular loop carryinig current I is located near an infinite long straight conductor carrying current I as shown in the figure. The loop,
Aremain stationaryBis attracted towards the wireCis repelled away from the wireDwill rotate about an axis parallel to the wireA rectangular coil pqrs is moved away from an infinite, straight wire carrying a current as shown in figure. Which of the following statements is corrent ?
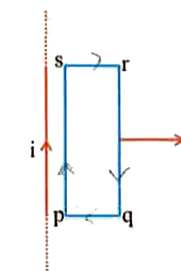AThere is no induced current in coil pqrsBThe induced current in coil pqrs is in the clockwise senseCThe induced current in the coil pqrs is in anticlockwise directionDnone of theseA long straight wire is parallel to one edge of a rectangular loop as shown in figure-5.310. if the current in the long wire varies with time as I=I0e−tr, what will be the induced emf in the loop at t=τ?
Aμ0bIπτIn(d+ad)Bμ0bI2πτIn(d+ad)C2μ0bIπτIn(d+ad)Dμ0bIπτIn(dd+a)
A rectangular loop of length 'l' and breadth 'b' is placed at a distance of x from an infinitely long wire carrying current 'i' such that the direction of current is parallel to breadth. If the loop moves away from the current wire in a direction perpendicular to it with a velocity 'v', the magnitude of the e.m.f. in the loop is: (μ0= permeability of free space)
View SolutionConsider an infinitely long wire carrying a current I (t),
With dIdt=λ = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig
View SolutionA rectangular loop of wire shown below is coplanar with a long wire carrying current I.
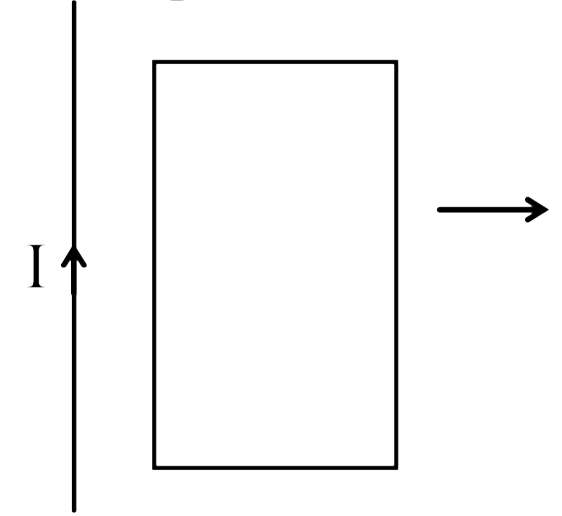The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop
View SolutionA rectangular loop of wire with dimensions shown in figure is coplanar with a long wier carrying current 'I'. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
View SolutionA circular loop of wire s in the same plane as an infinitely long wire carrying a constant current i. Four possible motions of the loop are marked by N, E, W, and S as shown.
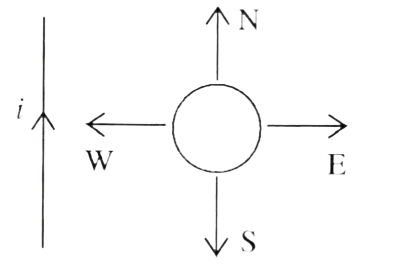
A clockwise current is induced in the loop when loop is pulled towards
View Solution