A wire of resistance 0.1 cm−1 bent to form a square ABCD of side 10 cm. A simailar wire is connected between the corners B and D to form the diagonal BD. Find the effective resistance of this combination between cornaers A and C. If a 2V battery of negligible internal resistance is connected across A and C calculate the total power dissipated.
1Ω,3W
1Ω,4W
2Ω,3W
2Ω,4W
The correct Answer is:B
To solve the problem, we need to find the effective resistance between points A and C in the given circuit configuration and then calculate the total power dissipated when a 2V battery is connected across A and C.
Step 1: Calculate the resistance of each segment of the wire
The resistance of the wire is given as 0.1cm−1 and the length of each side of the square is 10cm.
The resistance R of each side of the square can be calculated using the formula:
R=resistance per unit length×length
R=0.1cm−1×10cm=1Ω
Step 2: Identify the configuration of the resistances
In the square ABCD, we have:
- RAB=1Ω
- RBC=1Ω
- RCD=1Ω
- RDA=1Ω
Additionally, there is a wire connecting points B and D (the diagonal), which also has a resistance of 1Ω.
Step 3: Analyze the circuit
The resistances RAB and RDA are in series with the parallel combination of RBC, RCD, and the diagonal RBD.
Step 4: Calculate the equivalent resistance between A and C
The resistances RBC and RCD are in parallel with RBD. The equivalent resistance Req1 of RBC and RCD can be calculated as:
1Req1=1RBC+1RCD=11+11=2
Req1=12Ω
Now, we have Req1 in parallel with RBD:
1Req2=1Req1+1RBD=10.5+11=2+1=3
Req2=13Ω
Finally, the total resistance RAC between points A and C is:
RAC=RAB+RDA+Req2=1+1+13=2+13=73Ω
Step 5: Calculate the total power dissipated
Using the power formula:
P=V2R
where V=2V and R=73Ω:
P=(2)273=473=4×37=127W≈1.71W
Final Answer
The effective resistance between corners A and C is 73Ω and the total power dissipated is approximately 1.71W.
The resistance of the wire is given as 0.1cm−1 and the length of each side of the square is 10cm.
R=resistance per unit length×length
R=0.1cm−1×10cm=1Ω
In the square ABCD, we have:
- RAB=1Ω
- RBC=1Ω
- RCD=1Ω
- RDA=1Ω
The resistances RAB and RDA are in series with the parallel combination of RBC, RCD, and the diagonal RBD.
The resistances RBC and RCD are in parallel with RBD. The equivalent resistance Req1 of RBC and RCD can be calculated as:
1Req1=1RBC+1RCD=11+11=2
Req1=12Ω
1Req2=1Req1+1RBD=10.5+11=2+1=3
Req2=13Ω
RAC=RAB+RDA+Req2=1+1+13=2+13=73Ω
Using the power formula:
P=V2R
where V=2V and R=73Ω:
P=(2)273=473=4×37=127W≈1.71W
The effective resistance between corners A and C is 73Ω and the total power dissipated is approximately 1.71W.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-3)
Explore 2 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise-2 (Part-1)
Explore 25 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-1)
Explore 46 Videos
- COMMUNICATION SYSTEMSBook:RESONANCEChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
Similar Questions
Knowledge Check
ABCD is a square of side 'a' metres and is made of wires of resistance x ohms//metre. Similar wires are connected across the diagonals AC and BD. The effective resistance between the ax corners A and C will be
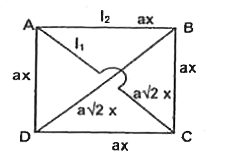 A(2−√2)axB6axC3axD(3−√2)ax
A(2−√2)axB6axC3axD(3−√2)axA uniform wire of 16Ω resistance is made into the form of a square. Two opposite corners of square are connected by a wire of resistance 16Ω. The effective resistance between the other two opposite corners is
A32ΩB16ΩC8ΩD4ΩA metallic wire of resistance 12Ω is bent to form a square. The resistance between two diagonal points would be
A12ΩB24ΩC6ΩD3Ω
ABCD is a square of side a meters and is mae up of wires of resistance xΩ/m. Similar wires are connected across the diagonals AC and BD. Show that the effective resistance of the frame-work between the corners A and C is (2−2√2 ax Ω.
View SolutionA square loop of total resistance 16 ohm. If a battery of 2V and 1ohm internal resistance is connected across one of its side then find potential difference across its diagnol
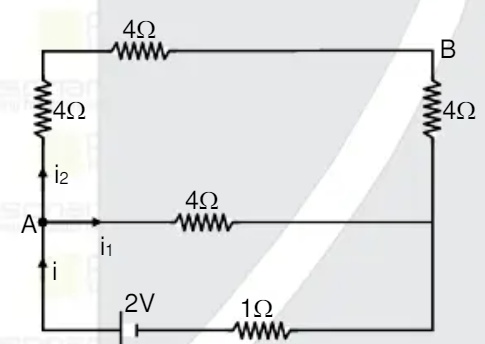
View SolutionA wire of resistance 15 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) A and D
View SolutionFour resistors are connected as shown in the figure. A 6 V battery of negligible resistance is connected across terminal battery of negligible resistance A and C. The potential difference across terminal B and D will be
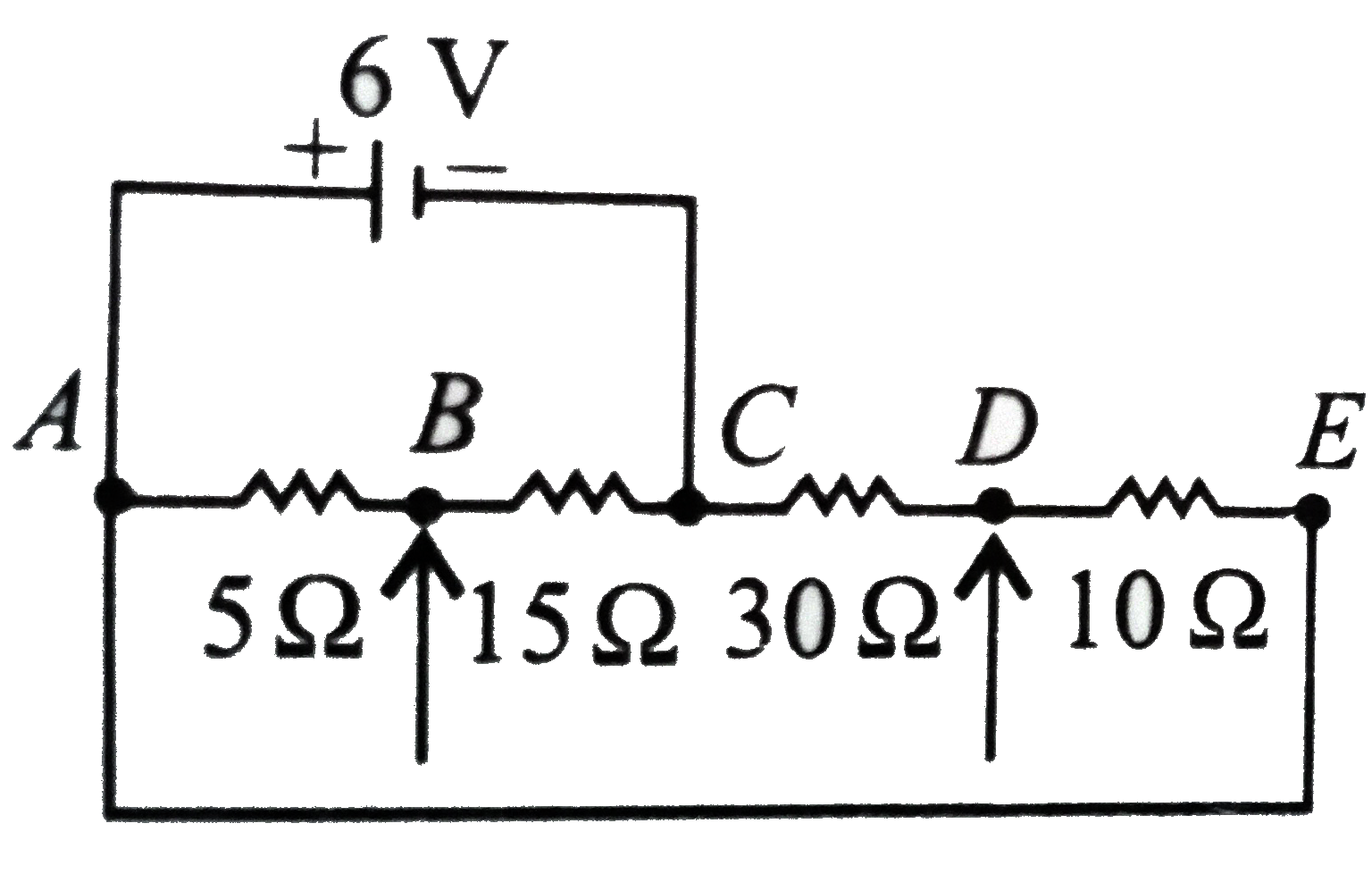
View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View Solution
