Question

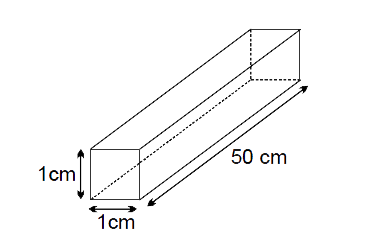
A rectabgykar carbon block has dimensions $1.0cm\times 1.0\times 50cm$.
(i) What is the resistance measured between the two square ends ?
(ii) Between two opposing rectangular faces ?
Resistivity of carbon at ${20}^{\circ }C\text{is}3.5\times {10}^{-5}\Omega m$.

Answer

(i)`R=(0.35)/2=0.175Omega`
`R=7xx10^(-5)Omega`

Explanation

To solve the problem, we will calculate the resistance of a rectangular carbon block in two scenarios: (i) between the two square ends and (ii) between the two opposing rectangular faces.

Given Data:
- Dimensions of the carbon block:
- Width (w) = 1.0 cm = 0.01 m
- Height (h) = 1.0 cm = 0.01 m
- Length (l) = 50.0 cm = 0.50 m
- Resistivity of carbon (ρ) = $$3.5\times {10}^{-5}\Omega \cdot m$$

(i) Resistance between the two square ends:
1. Identify the length and area:
- Length (l) = 50 cm = 0.50 m
- Area (A) = width × height = $$1.0cm\times 1.0cm=0.01m\times 0.01m=0.0001m^2$$

2. Use the resistance formula:
\( R = \frac{\rho \cdot l}{A} \)

3. Substitute the values:
\( R = \frac{3.5 \times 10^{-5} \, \Omega \cdot m \times 0.50 \, m}{0.0001 \, m^2} \)

4. Calculate the resistance:
\( R = \frac{1.75 \times 10^{-5} \, \Omega \cdot m^2}{0.0001 \, m^2} = 0.175 \, \Omega \)

(ii) Resistance between the two opposing rectangular faces:
1. Identify the length and area:
- Length (l) = 1 cm = 0.01 m (the distance between the two opposing rectangular faces)
- Area (A) = length × height = \(50.0 \, cm \times 1.0 \, cm = 0.50 \, m \times 0.01 \, m = 0.005 \, m^2\)

2. Use the resistance formula:
\( R = \frac{\rho \cdot l}{A} \)

3. Substitute the values:
\( R = \frac{3.5 \times 10^{-5} \, \Omega \cdot m \times 0.01 \, m}{0.005 \, m^2} \)

4. Calculate the resistance:
\( R = \frac{3.5 \times 10^{-7} \, \Omega \cdot m^2}{0.005 \, m^2} = 7 \times 10^{-5} \, \Omega \)

Summary of Results:
- (i) Resistance between the two square ends: \(0.175 \, \Omega\)
- (ii) Resistance between the two opposing rectangular faces: \(7 \times 10^{-5} \, \Omega\)