Find the capacitance between A and B if three dielectric slabs of dielectric constants A _(2)d_(2)d_(1)=d_(2)+d_(2).)
 .
.
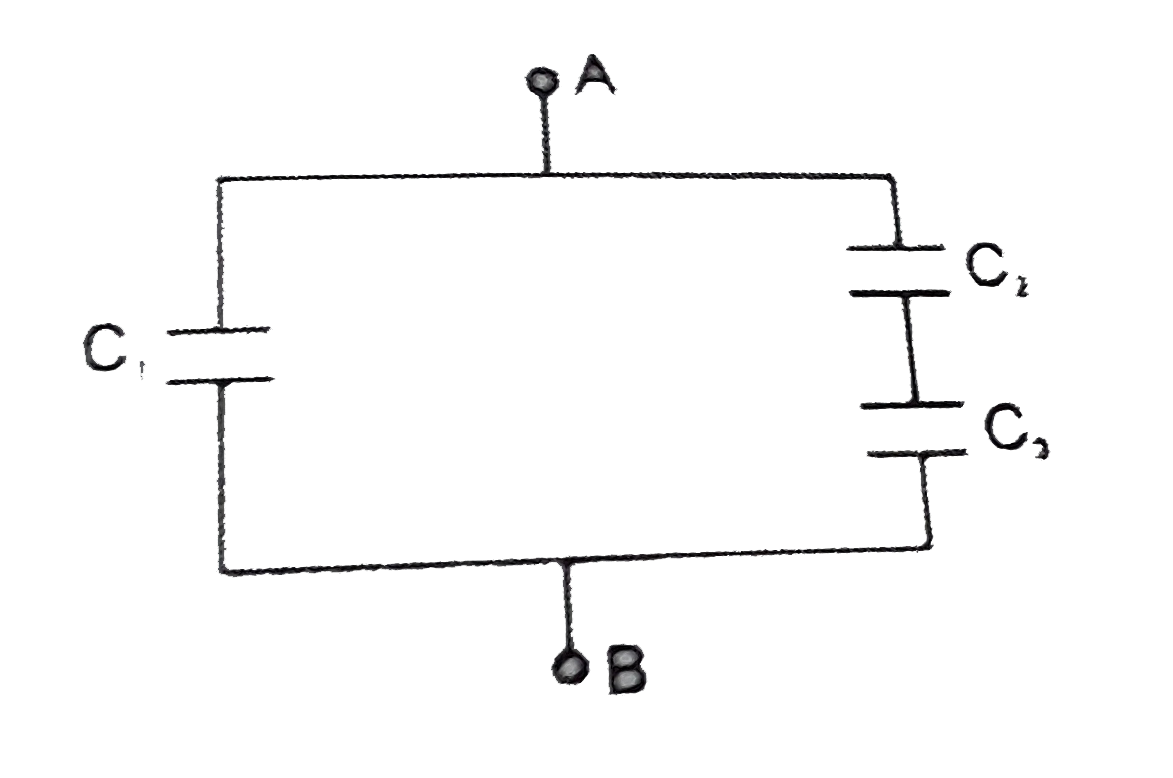
It is equivalent to
Topper's Solved these Questions
- CAPACITANCEBook:RESONANCEChapter:CAPACITANCEExercise:Miscellaneous Solved Example
Explore 3 Videos
- CAPACITANCEBook:RESONANCEChapter:CAPACITANCEExercise:Exercise - 1
Explore 79 Videos
- ATOMIC PHYSICSBook:RESONANCEChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
- COMMUNICATION SYSTEMSBook:RESONANCEChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
Similar Questions
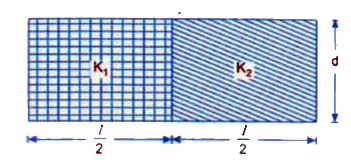
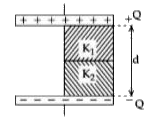
Two dielectric slabs of dielectric constants K1andK2 are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View Solution
Knowledge Check
Find the capacitance between A and B if two dielectric alabs (each of area A) of dielectric constants K1 and K2 and thicknesses d1 and d2 are inserted between the plates of a parallel plate capacitor of plate area A.
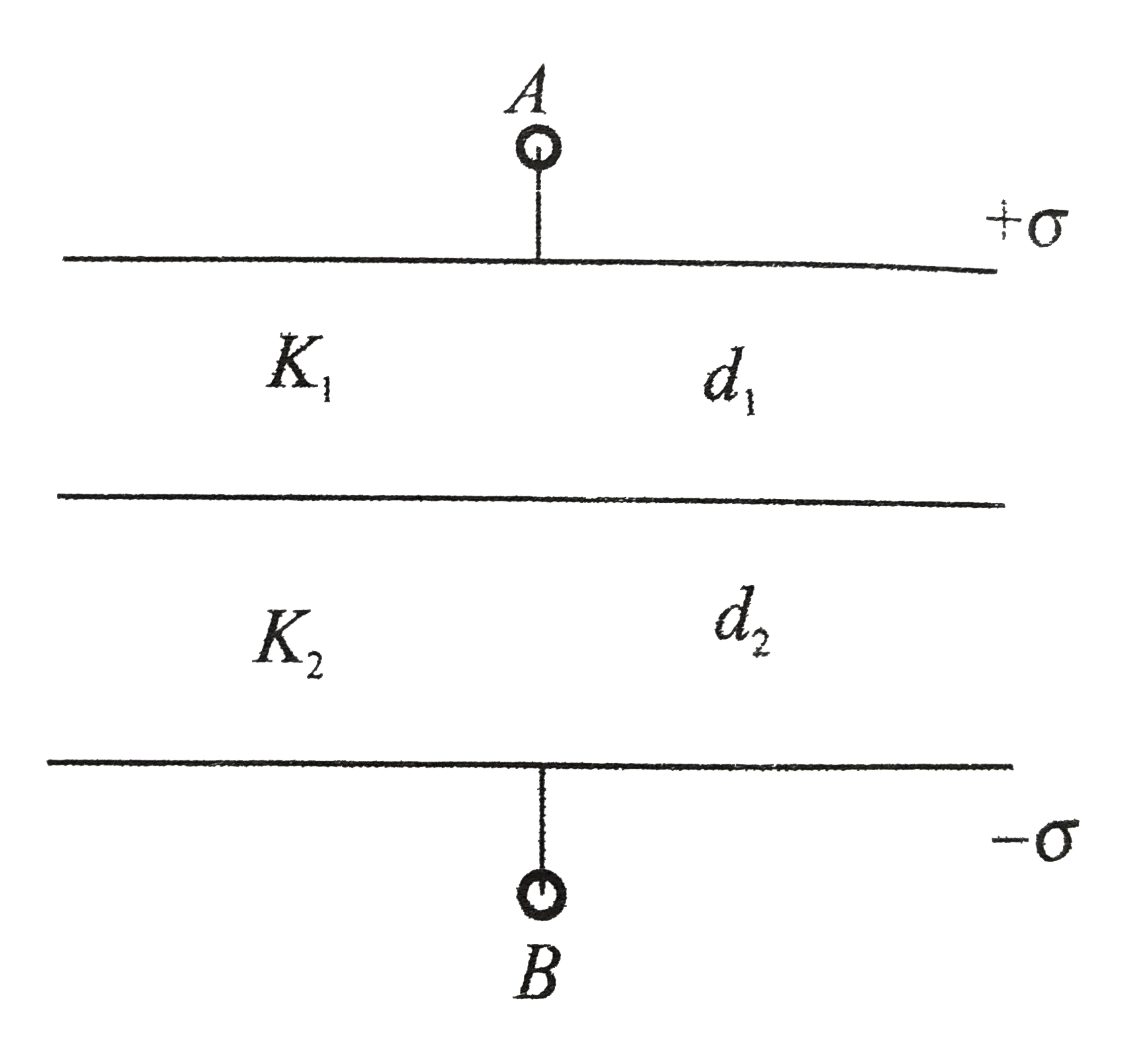 .AC=Aε0[K1K2K2d1+K1d1]BC=2Aε0[K1K2K2d1+K1d2]CC=Aε0[K1K22K2d1+K1d2]DC=Aε0[K1K2K2d1+K1d2]
.AC=Aε0[K1K2K2d1+K1d1]BC=2Aε0[K1K2K2d1+K1d2]CC=Aε0[K1K22K2d1+K1d2]DC=Aε0[K1K2K2d1+K1d2]Find the capacitance between A and B if two dielectric slabs (each of thickness d) of dielectric constants K1 and K2 and areas K1 and K2 and inserted between the plates of a parallel plate capacitor of plate area A.
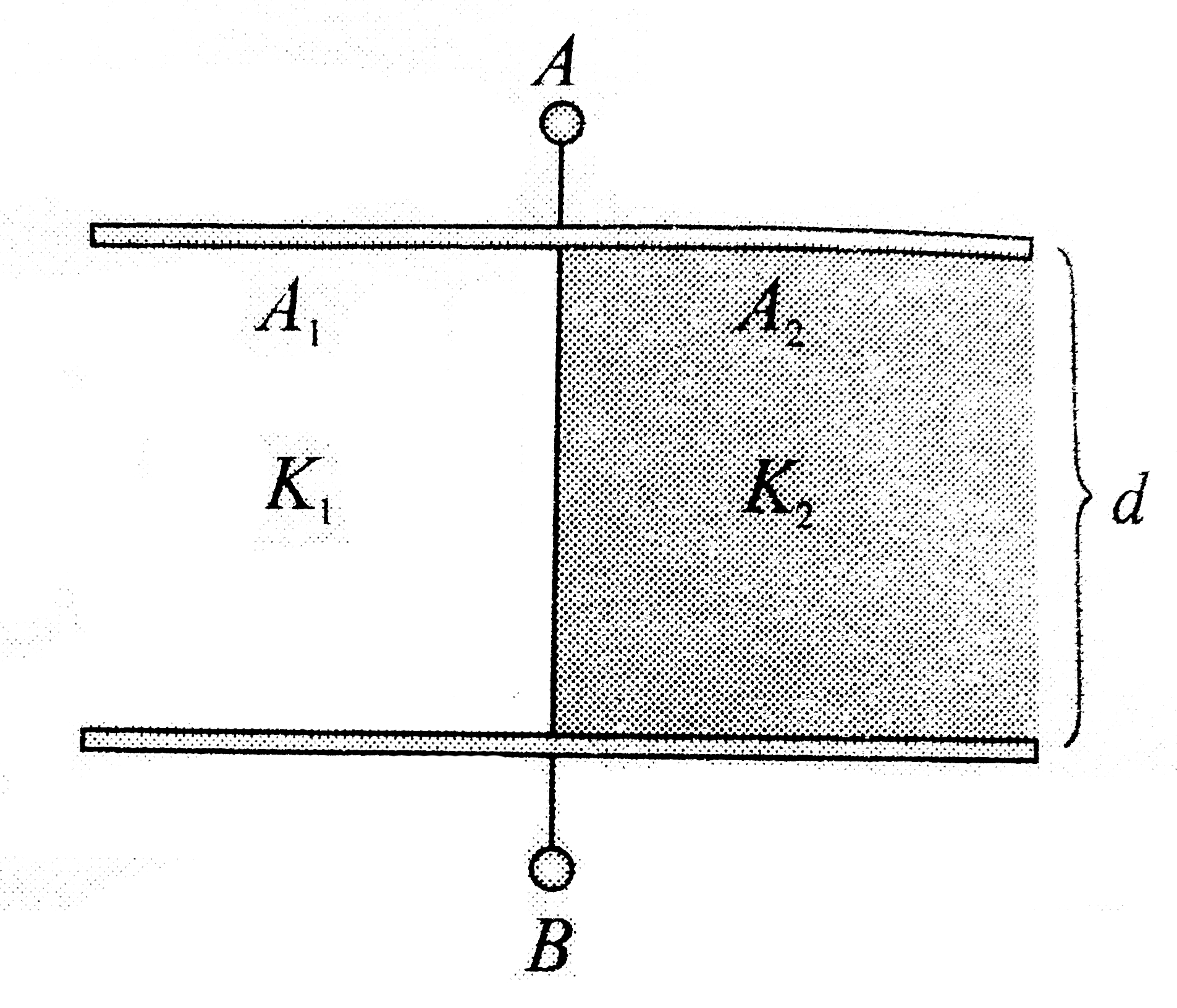 .ACequivalent=K1ε0A2d=ε0d(K1A1+K2A1)BCequivalent=ε0d(K2A1+K2A2)CCequivalent=K1ε0A2d=ε0d(K1A1+K2A2)DCequivalent=K1ε0A2d=ε0d(K1A1+K22A2)
.ACequivalent=K1ε0A2d=ε0d(K1A1+K2A1)BCequivalent=ε0d(K2A1+K2A2)CCequivalent=K1ε0A2d=ε0d(K1A1+K2A2)DCequivalent=K1ε0A2d=ε0d(K1A1+K22A2)A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases
The distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionA parallel-plate capacitor with plate area A has separation d between the plates. Two dielectric slabs of dielectric constant K1 and K2 of same area A/2 and thickness d/2 are inserted in the space between the plates. The capacitance of the capacitor will be given by :
View SolutionTwo thin dielectric slabs of dielectric constants K1 and K2(K1<K2) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by

View SolutionTwo material having the dielectric constans K1 and K2 are filled between two parallel plates of a capacitor.
where area of each plate is A and the distance between the plates is d.
The capacitor of the capacitor is:

View SolutionA metallic plate of thickness (t) and face area of one side (A) is inserted between the plates of a parallel plate air capacitor with a separation (d) and face are (A). Then the equivalent capacitance is
View Solution
