The instantaneous voltages at three terminals marked X, Y and Z are given by
VX=V0sinωt,VY=V0sin(ωt=2π3)andVz=V0sin(ωt=4π3)
An ideal voltmeter is configured to read runs value of the potential difference between its terminals. is connected between points X and Y and then between Y and Z. The reading the voltmeter will be
VX=V0sinωt,Vγ=V0sin(ωt+2π3)andVZ=V0sin(ωt+4π3)
VrmsXY=V0√32
VrmsYZ=V0√12
indpependent of the choice of the two terminals
The correct Answer is:A, C
Step by step video, text & image solution for The instantaneous voltages at three terminals marked X, Y and Z are given by V_(X)=V_(0)sin omegat, V_(Y)=V_(0)sin (omegat=(2pi)/(3))and V_(z)=V_(0)sin (omegat=(4pi)/(3)) An ideal voltmeter is configured to read runs value of the potential difference between its terminals. is connected between points X and Y and then between Y and Z. The reading the voltmeter will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCEChapter:ALTERNATING CURRENTExercise:PART-II
Explore 6 Videos
- ALTERNATING CURRENTBook:RESONANCEChapter:ALTERNATING CURRENTExercise:HIGH LEVEL PROBLEMS
Explore 11 Videos
- ALTERNATING CURRENTBook:RESONANCEChapter:ALTERNATING CURRENTExercise:PART-IV Comprehension
Explore 11 Videos
- ATOMIC PHYSICSBook:RESONANCEChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
Similar Questions
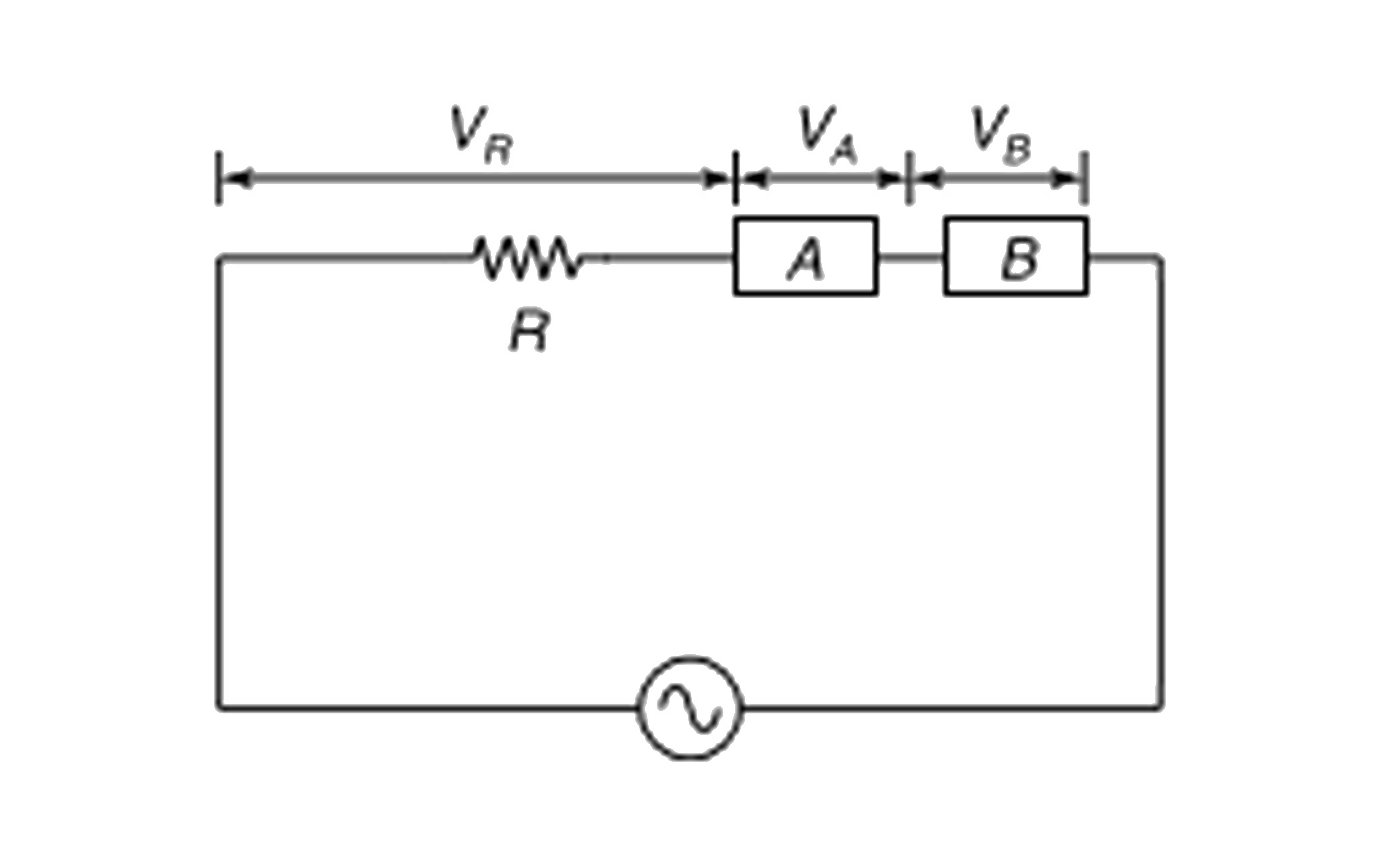
In the circuit shown in the Figure, the voltage across resistance R, box A and box B are represented as
vR=vsin(ωt),vA=√2Vsin(ωt+π4)and
vB=vsin(ωt+π2)Find the phase difference between current and the applied voltage.
View SolutionThree travelling waves are superimposed. The equations of the wave are
y!=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) and y3=4A0cos(kx−ωt)
find the value of ϕ(given 0≤ϕ≤π/2) if the phase difference between the resultant wave and first wave is π/4
View Solution
Knowledge Check
The instantaneous voltages at three terminals marked X, Y and Z are given by [
Vx=V0sinωt,
VY=V0sin(ωt+2π3) and
VZ=V0sin(ωt+4π3)
An ideal voltmeter is configured to read rms value of the potential difference between its terminals. It is connected between points X and Y and then between Y and Z. The reading(s) of the voltmeter will beAindependent of the choice of the two terminalsBVrmsxy=V0CVrmsyz=V0√12DVrmsxy=V0√32The instananeous voltages at three terminals marked X,Y and Z are given by
v
VY=V0sin(ωt+2π3)andVZ=V0sin(ωt+4π3).
An ideal volmeter is configured to read rms value of the potential difference between its terminal. It is connected between points X and Y and then between Y and Z. The reading(s) of the voltmeter will beAVrmXY=V0√32BVrmXY=V0√12CVrmXY=V0Dindependent of the choice og the two terminalsA,B and C are voltmeters of resistances R,1.5R and 3R respectively. When some potential difference is applied between x and y the voltmeter readings are VA,V_BandV_C, then
 AVA=VB=VCBVA≠VB=VCCVA=VB≡VCDVA+VB=VC
AVA=VB=VCBVA≠VB=VCCVA=VB≡VCDVA+VB=VC
Three travelling waves are superimposed. The equations of the wave are
y!=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) and y3=4A0cos(kx−ωt)
find the value of ϕ(given 0≤ϕ≤π/2) if the phase difference between the resultant wave and first wave is π/4
View SolutionWhat is the power dissipation in an AC circuit in which voltage and current are given by V=300sin(ωt+π2) and I = 5 sinωt ?
View SolutionA voltmeter reads the potential difference across the terminals of an old battery as 1.40V, while a potentiometer reads its voltage to be 1.55V. The voltmeter resistance is 280Ω.
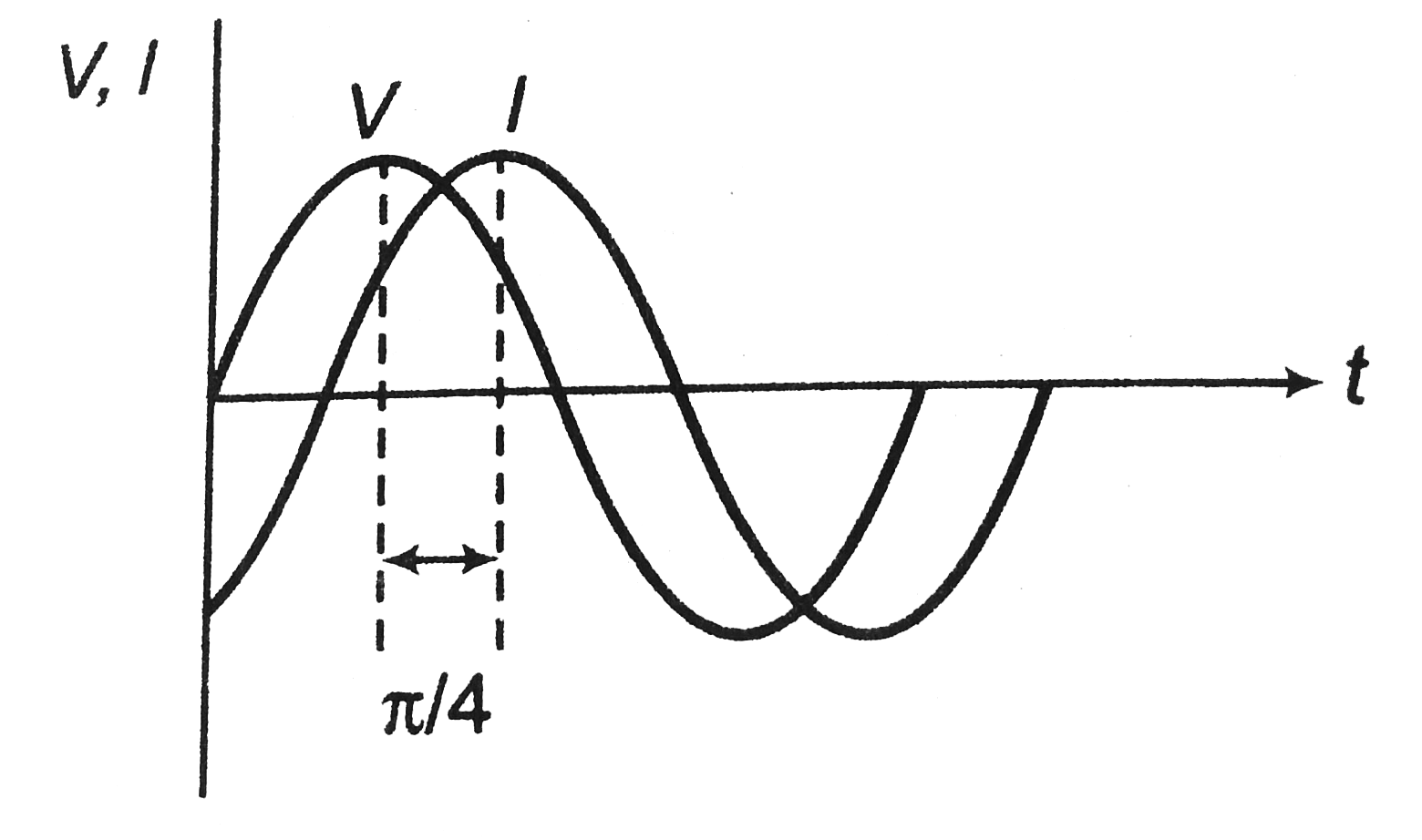
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .
.
View SolutionThe voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle is
View Solution