A curve passes through the origin. Through any point on the curve, lines are drawn parallel to the co-ordinate axes. If the curve divides the area formed by these lines and co-ordinates axes in the ratio find the curve.
Area
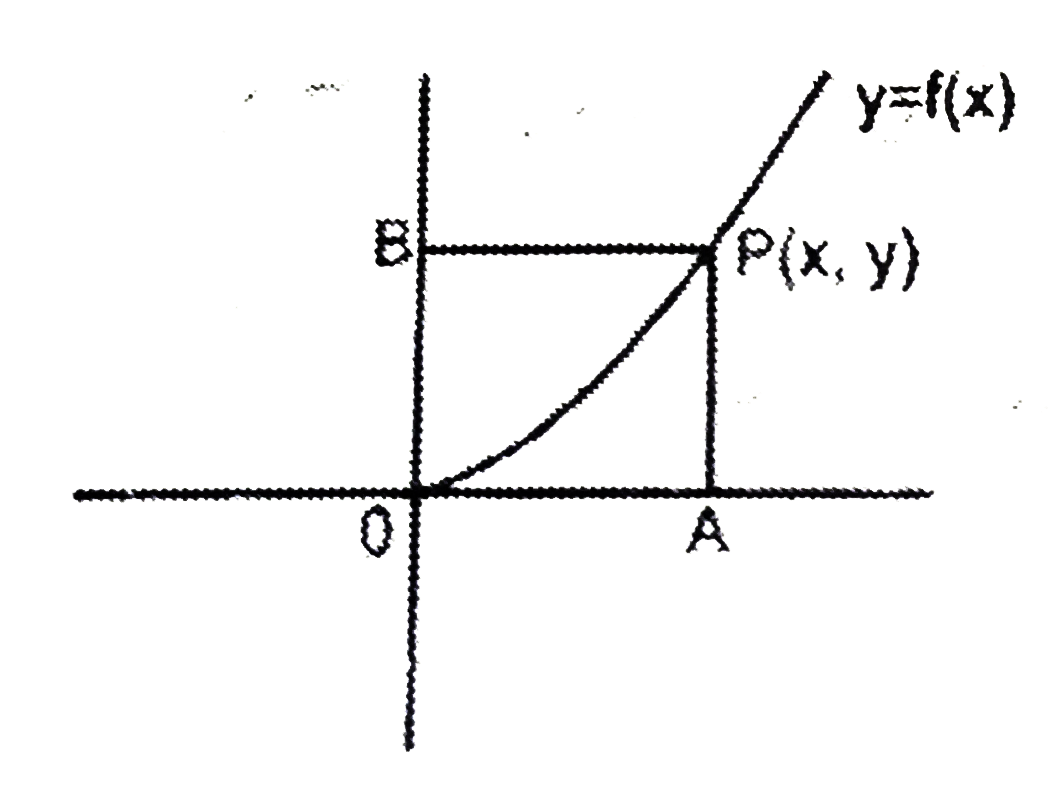
Area
Differentiating w.r.t x
similarly
Topper's Solved these Questions
- DEFINITE INTEGRATION & ITS APPLICATION Book:RESONANCEChapter:DEFINITE INTEGRATION & ITS APPLICATION Exercise:Self practive problem
Explore 56 Videos
- DEFINITE INTEGRATION & ITS APPLICATION Book:RESONANCEChapter:DEFINITE INTEGRATION & ITS APPLICATION Exercise:Exercise 1
Explore 31 Videos
- COMBINATORICSBook:RESONANCEChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 8 Videos
- DPPBook:RESONANCEChapter:DPPExercise:QUESTION
Explore 665 Videos
Similar Questions
A curve y=f(x) passing through origin and (2,4). Through a variable point P(a,b) on the curve,lines are drawn parallel to coordinates axes. The ratio of area formed by the curve y=f(x),x=0,y=b to the area formed by the y=f(x),y=0,x=a is equal to 2:1. Equation of line touching both the curves y=f(x)andy2=8x is
View SolutionFind the equation of lines drawn parallel to co-ordinate axes and passing through the point (−1,4).
View Solution
Knowledge Check
Through any point (x, y) of a curve which passes through the origin, lines are drawn parallel to the coordinate axes. The curve, given that it divides the rectangle formed by the two lines and the axes into two areas, one of which is twice the other, represents a family of
AcirclesBparabolasChyperbolasDstraight linesThrough any point (x, y) of a curve which passes through the origin, lines are drawn parallel to the coordinate axes. The curve, given that it divides the rectangle formed by the two lines and the axis into two areas, one of which is twice the other, represent a family of
AcirclesBparabolasChyperbolasDstraight linesIf the ordinate x=a divides the area bounded by the curve y=cos−1 x and axis of x. Then value of a is.
A2√3B2√2C3DNone of these
A normal at any point (x,y) to the curve y = f(x) cuts triangle of unit area with the axes, the equation of the curve is :
View SolutionA curve passage through the point (5,3) and at any point (x,y) on it, the product of its slope and the ordinate is equal to its abscissa. The curve is a/an
View SolutionCo-ordinates of a point on the curve y=xlogx at which at normal is parallel to the line 2x−2y=3 are
View SolutionWhat is the area between the curve
y=cos3x,0≤x≤π6 and the co-ordinate axes ?
View SolutionThe co-ordinates of the point of the curve y=x−4x, where the tangent is parallel to the line y=2x is
View Solution