Compare which of the two is greater (100)1100and(101)1101
Video Solution
Text Solution
Assume f(x) =x1/2 and let us examine monotonic nature of f(x)
f(x)=x1/2.(1−enxx2)
f(x)>0 ⇒ x∈(0,e)
and f(x)<0⇒x∈(e,∞)
Hence f(x) is M.D. For x≤e
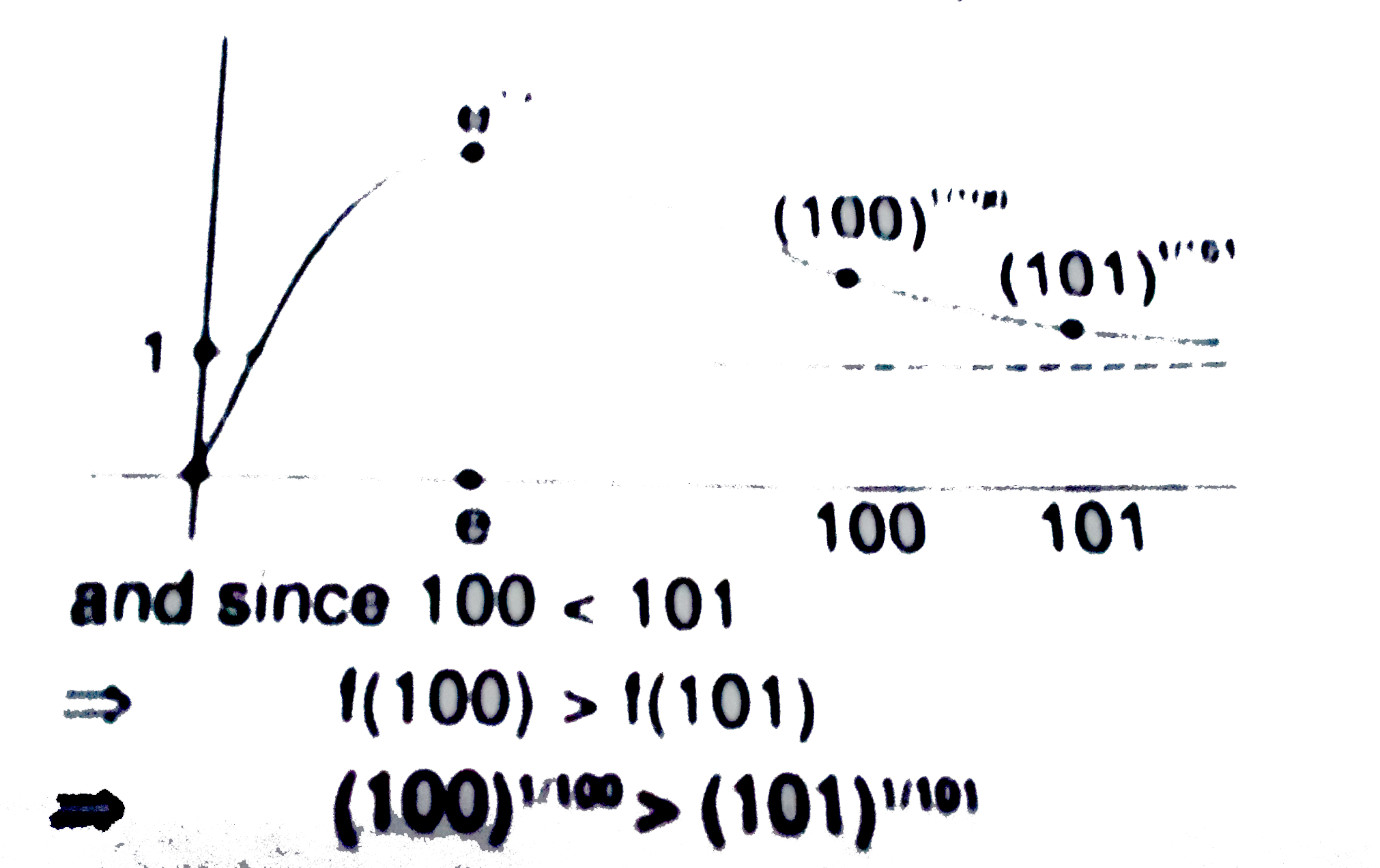
and since 1000<101
⇒f(100)>f(101)
⇒(100)1/100>(101)1/100
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems
34 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A
5 Videos
- COMBINATORICSBOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
8 Videos
Similar Questions
Knowledge Check
Larger of 9950+10050and10150 is ………..
A10150B9950+10050CBoth are equalDNone of theseIf sin−1x+sin−1y+sin−1z=3π/2, then the value of
x100+y100+z100−9x101+y101+z101 isA−1B0C1D3The number of terms in the expansion of (1+x)101(1+x2−x)100 in powers of x is:
A101B202C301D302
Which is larger : (9950+10050) or (101)50.
View SolutionLarger of 9950+10050and10150 is ………..
View SolutionIf sin−1x+sin−1y+sin−1z=3π2 then the value of x100+y100+z100−3x101+y101+z101 is
View SolutionIf sin−1x+sin−1y+sin−1z=3π2 then the value of x100−y100−z100−12x101−y101−z101=
View SolutionThe sum of the series C(101,1)C(101,0)+2C(101,2)C(101,1)+3C(101,3)C(101,2)+...+101C(101,101)C(101,100)=
View Solution