Prove that $ln (1 + \frac{1}{x}) > \frac{1}{1 + x}, x > 0$ . Hence, show that the function $f (x) = {(1 + \frac{1}{x})}^{x}$ strictly increases in $(0, \infty)$ .

Video Solution

Text Solution

Verified by Experts

$f (x) - {(1 + \frac{1}{x})}^{x} for Domain of f (x) 1 + \frac{1}{x} l > 0$
$\Rightarrow \frac{x + 1}{x} > 0 \Rightarrow (- \infty, - 1) \cup (0, \infty)$
$Consider f (x) = {(1 + \frac{1}{x})}^{2} [e n (1 + \frac{1}{x}) + \frac{x}{1 + \frac{1}{x}} . \frac{- 1}{x^{2}}]$
$\Rightarrow f (x) = {(1 + \frac{1}{x})}^{x} [e n (1 + \frac{1}{x}) - \frac{1}{x + 1}]$
Now ${(1 + \frac{1}{x})}^{x}$ is always positive , hence the sigh of f(x) depends on sigh of $e n (1 + \frac{1}{x}) - \frac{1}{1 + x}$ i.e., we have to compare en $(1 + \frac{1}{x})$ and So lets assume g (x) $= e n (1 + \frac{1}{x}) - \frac{1}{x + 1}$
$g (x) = \frac{1}{1 + \frac{1}{x}} . \frac{- 1}{x^{2}} + \frac{1}{{(x + 1)}^{2}} \Rightarrow g (x) = \frac{- 1}{x {(x + 1)}^{2}}$
$(i) for x \in (0, \infty), g (x) < 0 \Rightarrow g (x) is M . D for x \in (0, \infty)$
$g (x) < lim x \to \infty g (x)$
$g (x) > 0 and since g (x) > 0 \Rightarrow f (x) > 0$
$(i i) for x \in (- \infty, - 1) g (x) > 0 \Rightarrow g (x) is M . I . for x \in (- \infty, - 1)$
$\Rightarrow g (x) > lim x \to \infty g (x) \Rightarrow g (x) > 0 \Rightarrow f (x) > 0$
Hence from (i) and (ii) we get f(x) $>$ 0 for all $x \in (- \infty, - 1) \cup (0, \infty)$
$\Rightarrow f (x)$ is M.I. in its Domain
For drawing the graph of f(x) its important to find the value of f(x) at boundary points i.e., $\pm \infty, 0, - 1$
$lim x \to \infty {(1 + \frac{1}{x})}^{x} = e$
$lim x \to 0 {(1 + \frac{1}{x})}^{x} = 1 and lim x \to - 1 {(1 + \frac{1}{x})}^{x} = \infty$

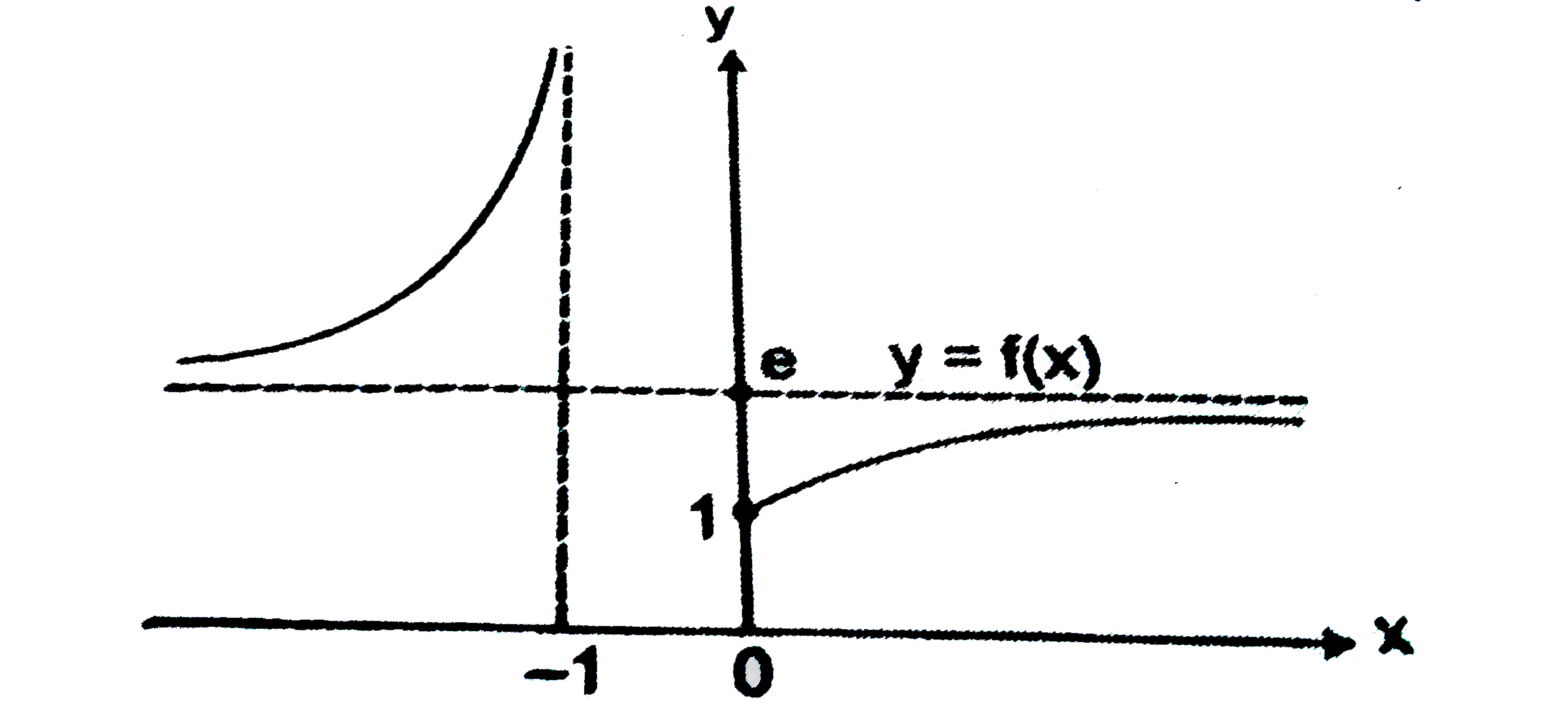
so the graph of f(x) is
Range is $y \in (1, \infty) - {e}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

RESONANCE-APPLICATION OF DERIVATIVES-High Level Problems (HLP)

Home
Ask Doubt
Profile