Find points of local maxima or minima of
f(x) =x5−5x4+5x3−1
Video Solution
Text Solution
f(x)=x5−5x4+5x3−1
f(x)=5x2(x−1)(x−3)
f(x)=0 ⇒ x=0,1,3
f''(x)=10x(2x2−6x+3)
Now f''(1)<0 ⇒ Maxima at x=1
f''(3)>0 ⇒ Minima at x=3
and f''(0)=0 ⇒ IInd dervative test fails
So f'''(x)=30(2x2−4x+1)
f'''(0)=30
⇒ Neither maxima nor minima at x=0
Note : It was very convenient to check maxima/minima at first step by examining the sigh change of f(x) no sigh change of f'(x) at x=0
f'(x)=5x2(x−1)(x−3)
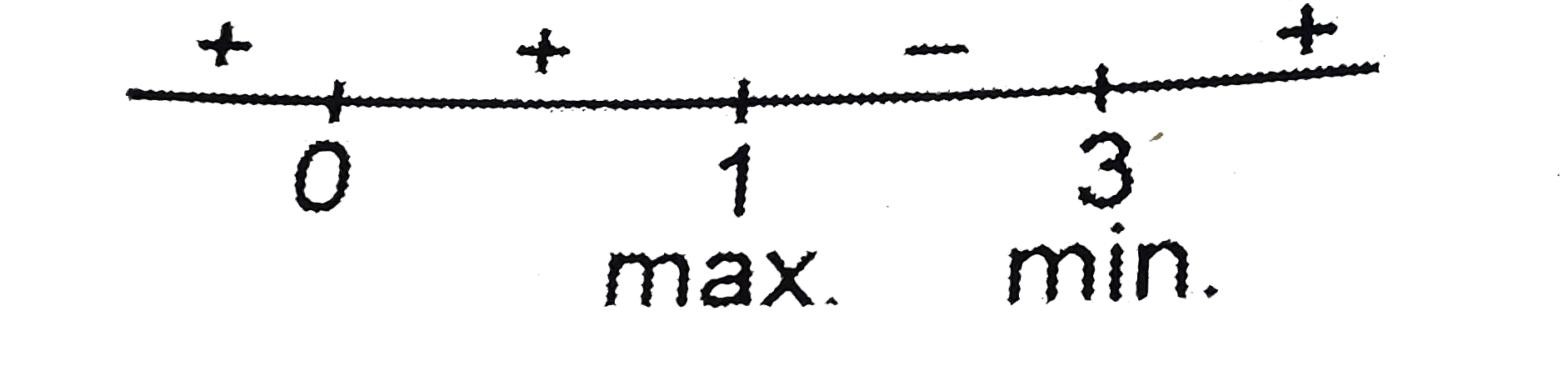
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:RESONANCEChapter:APPLICATION OF DERIVATIVESExercise:Self Practice Problems
Explore 34 Videos
- APPLICATION OF DERIVATIVESBook:RESONANCEChapter:APPLICATION OF DERIVATIVESExercise:Exersise -1A
Explore 5 Videos
- COMBINATORICSBook:RESONANCEChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 8 Videos
Similar Questions
Knowledge Check
The points of local maxima or local minima of the function f(x)=x3+x2+x+1 are:
A0, 1, 1B−1,0,1C−1,−1,0DDoes not exist
Find all the points of local maxima and minima of the f(x)=x3−6x2+9x−8
View SolutionFind the points of local maxima/minima of function
f(x)=xlnx
View SolutionFind the points of local maxima/minima of function
f(x)=2x3−21x2+36x−20
View SolutionFind the points of local maxima/minima of function
f(x)=−(x−1)3(x+1)2
View SolutionFind the points of local maxima and minima of the function f(x)=x2−4x.
View SolutionFind the points of local maxima or minima for f(x)= sin 2x−x,x∈(0,π)
View SolutionFind all the points of local maxima and minima of the function f(x)=x3−6x2+9x+15 .
View Solution

