If area of circle increases at a rate of 2cm2/sec then find the rate at which area of the inscribed square increases.
Area of circle ,A,=πr2. Area of square ,A2=2r2 (see figure)
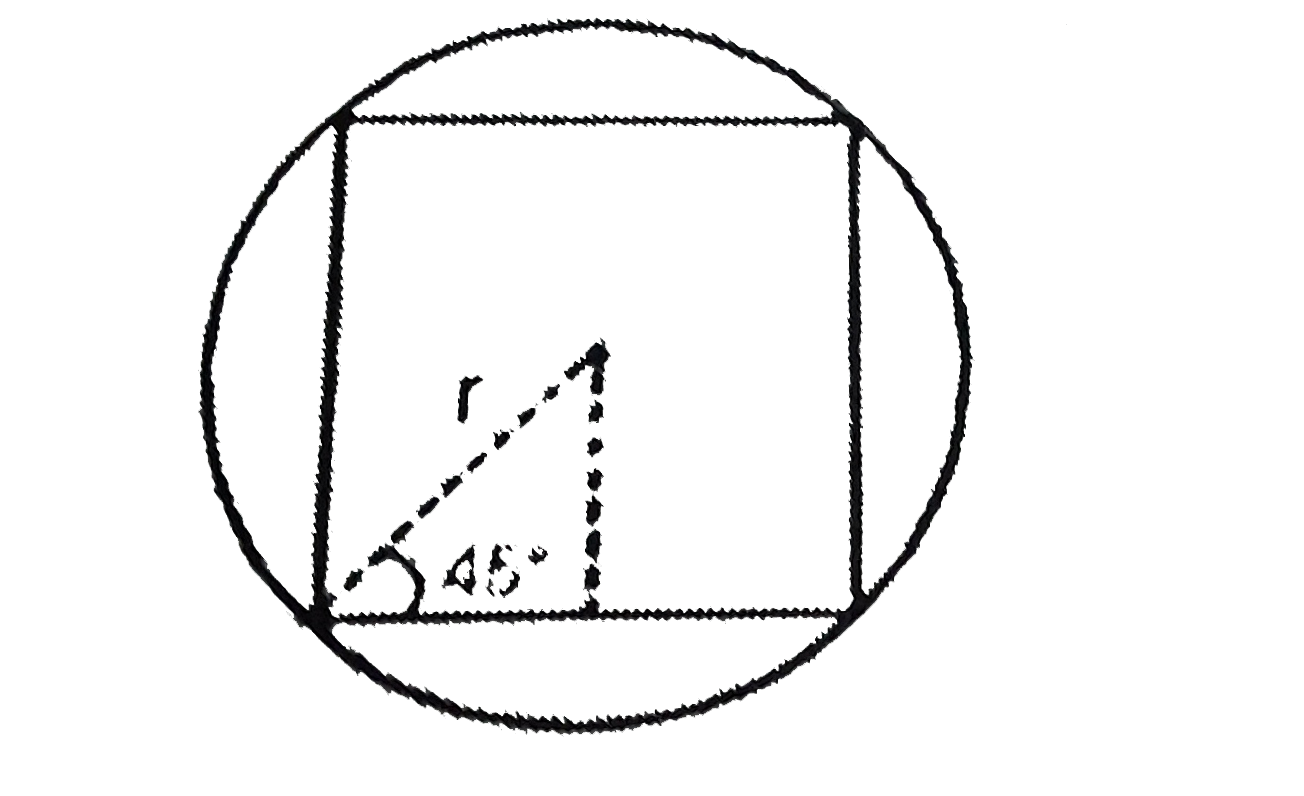
dAdt,=2πr.drdt dA2dt=4r.drdt
∵ 2=2πr.drdt ⇒ rdrdt=1π
∴dA2dt=4.1π=4π.cm2/sec
Area of square increases at the rate .4πcm2/sec.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:RESONANCEChapter:APPLICATION OF DERIVATIVESExercise:Self Practice Problems
Explore 34 Videos
- APPLICATION OF DERIVATIVESBook:RESONANCEChapter:APPLICATION OF DERIVATIVESExercise:Exersise -1A
Explore 5 Videos
- COMBINATORICSBook:RESONANCEChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 8 Videos
Similar Questions
The radius of a circle is increasing uniformly at the rate of 4 cm/sec. Find the rate at which the area of the circle is increasing when the radius is 8 cm.
View SolutionThe radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
View Solution
Knowledge Check
If the surface area of a cube increases at the rate of 0.6cm2/sec, then, when the side is 4 cm , volume of the cube is increasing at the rate of
A6c.c/sec.B60c.c/sec.C0.6c.c/sec.D0.06c.c/sec.The length of the side of a square sheet of metal is increasing at the rate of 4cm/sec. The rate at which the area of the sheet is increasing when the length of its side is 2cm, is
A16cm2/secB8cm2/secC32cm2/secD4cm2/sec
The radius of a circle is increasing uniformly at the rate of 3cm/s.Find the rate at which the area of the circle is increasing when the radius is 10 cm.
View SolutionIf the surface area of a cube increases at a rate of 24cm^2/s, then the rate at which its volume increases with respect to time if its side a=2cm, will be:
View SolutionRadius of a circle is increasing at rate of 3cm/sec Find the rate at which the area of circle is increasing at the instant when radius is 10 cm.
View SolutionIf the surface area of a cube increases at the rate of 0.6cm2/sec, then, when the side is 4 cm , volume of the cube is increasing at the rate of
View SolutionAn equilateral triangle's sides increase at the rate of 2cm/sec. If the area of its incircle increases at a rate of kcm2/sec (when the length of the side is 6πcm), then the value of k is
View SolutionIf the radius of a circle is increasing at a uniform rate of 2 cm/s, then find the rate of increase of area of circt the instant when the radius is 20 cm.
View Solution

