Find equation of tangent to y =ex at x=0 . Hence draw graph
Video Solution
Text Solution
Atx=0 ⇒ y=e0=1
dydx = ex ⇒ dydx∣x=0=1
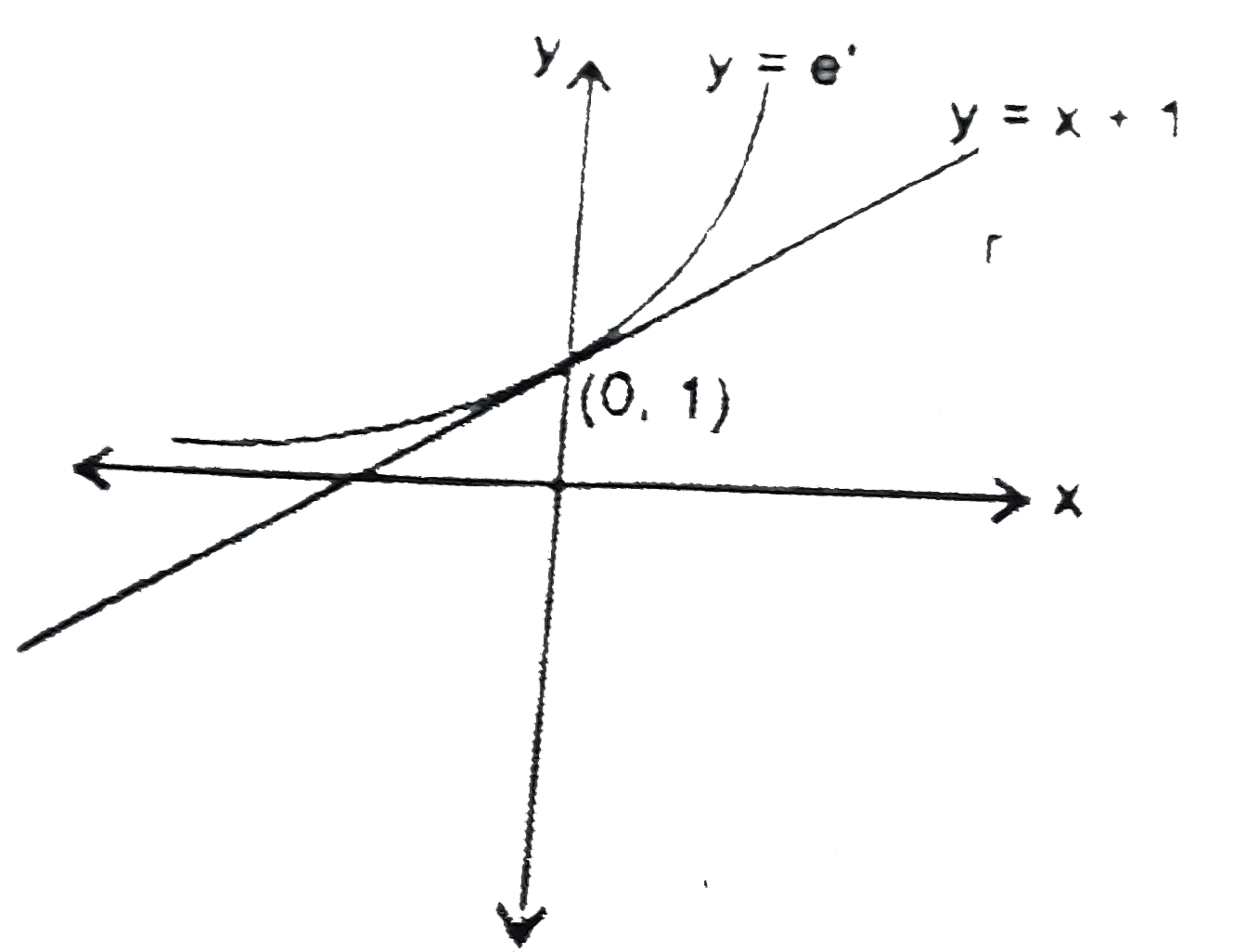
Hence equation of tangent is
1(x−0)=(y−1)
⇒ y=x+1
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems
34 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A
5 Videos
- COMBINATORICSBOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
8 Videos
Similar Questions
Knowledge Check
Equation of the tangent to the curve y=ex at (0,1) is
Ax=0By=1Cx+y=1Dx−y+1=0
Find an equation of the tangent line to the curve y=ex/(1+x2) at the point (1,e/2)
View SolutionDraw the graph of two lines whose equations are x+y−6=0andx−y−2=0, on the same graph paper. Find the area of triangle formed by the two lines and y axis.
View SolutionFind the equation of the tangent to the curvey={x2sin1x,x≠00,x=0aheorig∈
View SolutionFind number of vertical tangents to the curve y−exy+x=0
View SolutionSolve the differential equation. dydx−y=ex Hence find the particluar solution for x = 0 and y = 1 .
View SolutionDraw the graph of y=exsin2πx.
View SolutionDraw the graph of the equations x-y+1 = 0 and 3x + 2y - 12 = 0. Using this graph, find the values of x and y which satisfy both the equations.
View Solution