A mineral of iron contains an oxide containing 72.36% iron by mass and has a density of 5.2 g/cc. its unit cell is cubic with edge length of 839 pm. What is the total number of atoms (ions) present in each unit cell ? (Fe -56, O-16)
The correct Answer is:56
To solve the problem, we need to determine the total number of atoms (ions) present in the unit cell of the iron oxide mineral. Here's a step-by-step breakdown of the solution:
Step 1: Determine the Molar Mass of the Oxide
Given that the mineral contains 72.36% iron by mass, we can calculate the molar mass of the oxide.
Let the molar mass of the oxide be M. The mass fraction of iron is given by:
mass of Femass of oxide=0.7236
Let x be the mass of iron in the oxide, then the mass of the oxide is M. Thus:
56M=0.7236
Where 56 g/mol is the molar mass of iron (Fe). Rearranging gives:
M=560.7236≈77.5 g/mol
Step 2: Calculate the Mass of the Unit Cell
Using the density of the oxide (5.2 g/cc), we can find the mass of the unit cell.
The volume of the cubic unit cell can be calculated using the edge length:
Volume=a3=(839 pm)3=(839×10−10 cm)3=5.9×10−23 cm3
Now, using the density (ρ) to find the mass (m) of the unit cell:
m=ρ×Volume=5.2 g/cm3×5.9×10−23 cm3≈3.07×10−22 g
Step 3: Calculate the Number of Moles in the Unit Cell
To find the number of moles of the oxide in the unit cell, we use the molar mass calculated earlier:
Number of moles=mass of unit cellmolar mass=3.07×10−22 g77.5 g/mol≈3.96×10−24 mol
Step 4: Calculate the Number of Formula Units in the Unit Cell
Using Avogadro's number (NA=6.022×1023 mol−1), we can find the number of formula units in the unit cell:
Number of formula units=Number of moles×NA≈3.96×10−24 mol×6.022×1023 mol−1≈2.38 formula units
Step 5: Determine the Total Number of Atoms in the Unit Cell
Assuming the oxide is of the form FexOy, we can deduce the ratio of iron to oxygen. Given the oxide contains iron and oxygen, let’s assume it is Fe2O3 (common iron oxide).
Each formula unit Fe2O3 contains 2 Fe atoms and 3 O atoms, giving a total of:
Total atoms per formula unit=2+3=5 atoms
Thus, the total number of atoms in the unit cell is:
Total atoms in unit cell=2.38 formula units×5 atoms/formula unit≈11.9 atoms
Since the number of atoms must be a whole number, we round it to 12 atoms.
Final Answer
The total number of atoms (ions) present in each unit cell is approximately 12.
---
Given that the mineral contains 72.36% iron by mass, we can calculate the molar mass of the oxide.
Using the density of the oxide (5.2 g/cc), we can find the mass of the unit cell.
To find the number of moles of the oxide in the unit cell, we use the molar mass calculated earlier:
Using Avogadro's number (NA=6.022×1023 mol−1), we can find the number of formula units in the unit cell:
Assuming the oxide is of the form FexOy, we can deduce the ratio of iron to oxygen. Given the oxide contains iron and oxygen, let’s assume it is Fe2O3 (common iron oxide).
The total number of atoms (ions) present in each unit cell is approximately 12.
Topper's Solved these Questions
- SOLID STATEBook:RESONANCEChapter:SOLID STATEExercise:Part-III (One or more than one option correct type)
Explore 3 Videos
- S BLOCK ELEMENTSBook:RESONANCEChapter:S BLOCK ELEMENTSExercise:INORGANIC CHEMISTRY(s-Block Elements)
Explore 36 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBook:RESONANCEChapter:STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYExercise:Section -B
Explore 18 Videos
Similar Questions
An element crystallises in fcc crystal lattice and has a density of 10 g cm 3 with unit cell edge length of 100 pm. Calculate number of atoms present in 1 g of crystal.
View SolutionAn element crystallises in the fcc crystal lattice and has a density of 10 g cm−3 with unit cell edge length of 100 pm . Calculate number of atoms present in 1 g of crystal.
View Solution
Knowledge Check
A compound having bcc geometry has atomic mass 50. Calculate the density of the unit cell, if the edge length is 290pm.
A6.81gcm−3B3.40gcm−3C13.62gcm−3Dnone of theseFeO crystal has a simple cubic structure and each edge of the unit cell is 5 Å . Taking density of the oxide as 4g/cc, the number of Fe2+andO2− ions present in each unit cell are
A4Fe2+and4O2−B6Fe2+and6O2−C2Fe2+and2O2−D1Fe2+and1O2−Ferrous oxide has a cubic structure and each edge of the unit cell is 5.0 Å. Assuming density of the oxide as 4.0gcm2 then the number of Fe2+andO2− ions present in each unit cell will be
ATwo Fe2+and four O2−BThree Fe2+0and three O2−CFour Fe2+ and two O2−DFour Fe2+ and four O2−
An element having bcc geometry has atomic mass 50. Calculate density of unit cell if its edge length is 290 pm.
View SolutionA compound having bcc geometry has atomic mass 50. Calculate the density of the unit cell if its edge length is 290 pm.
View SolutionThe density of chormium is 7.2g cm−3. If the unit cell is a cube edge length of 298 pm, determine the type of the unit cell. (Atomic mass of Cr = 52 amu)
View SolutionPerovaskite, a mineral containing calcium, oxygen & titanium crystallizes in the given unit cell
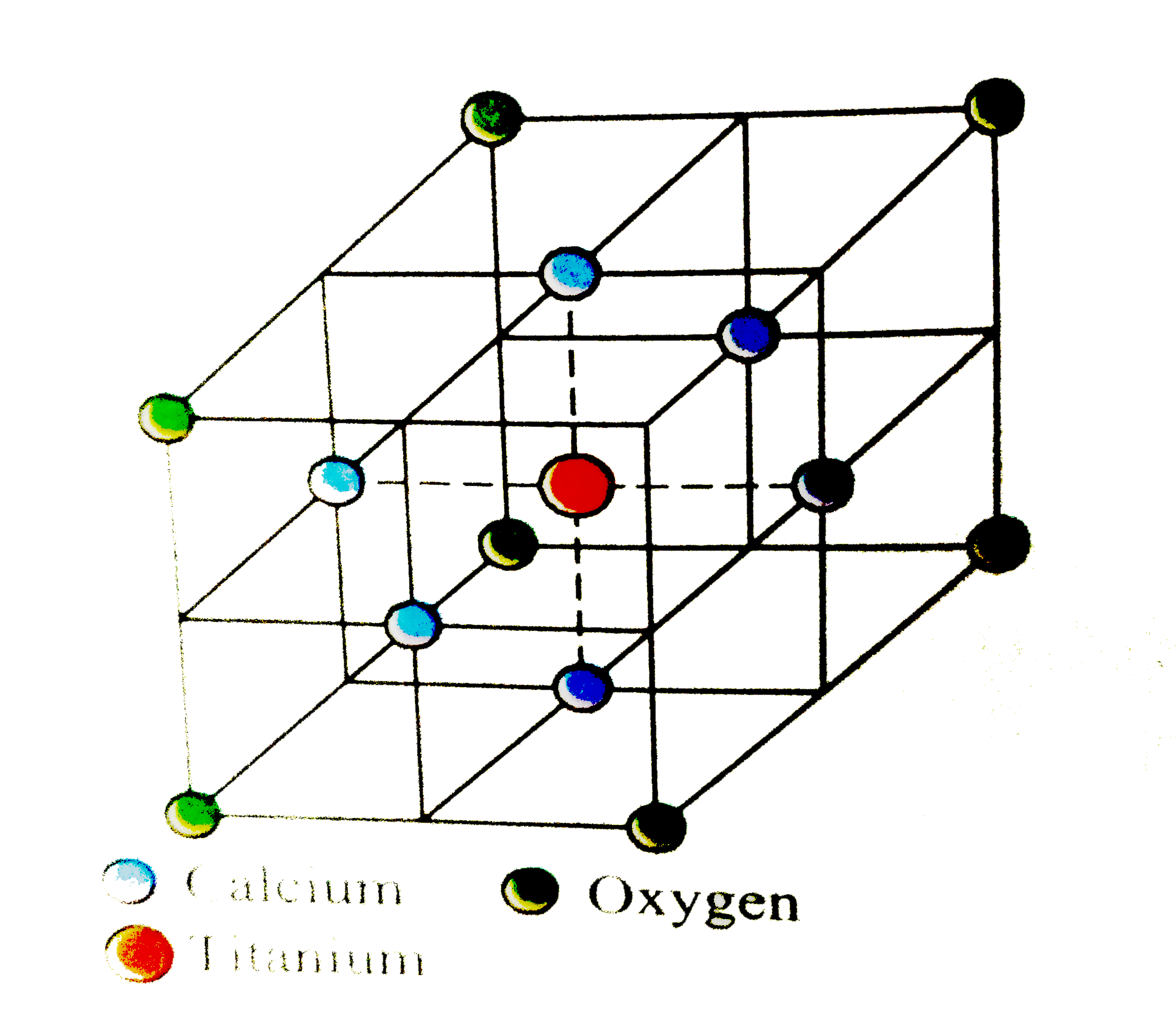
Total number of atom present in a unit cell is
View SolutionFerrous oxide has a cubic structure. The length of edge of the unit cell is 5 Å. The density of the oxide is 4.0gcm−3. Then the number of Fe2+andO2− ions present in each unit cell will be
View Solution

