The shortest distance between IstandVth layer of HCP arrangement is:
8√23r
4√32r
16√123r
8√32r
The correct Answer is:A
To find the shortest distance between the first and the fifth layer of a Hexagonal Close Packing (HCP) arrangement, we can follow these steps:
Step 1: Understand the HCP Structure
In an HCP structure, the layers are arranged in a specific manner. The first layer (A) is followed by the second layer (B), which is then followed by the third layer (A again), the fourth layer (B), and the fifth layer (A). The arrangement alternates between two types of layers.
Step 2: Identify the Distance Between Layers
The distance we are looking for is the vertical distance between the first layer (A) and the fifth layer (A). In HCP, the distance between two consecutive layers can be determined by the height of the tetrahedron formed by the atoms in the layers.
Step 3: Calculate the Height of a Tetrahedron
The height (h) of a tetrahedron can be calculated using the formula:
h=2√3R
where R is the radius of the atoms in the structure.
Step 4: Calculate the Total Distance
Since the distance between the first layer and the fifth layer involves moving through four heights (from the first layer to the second, second to the third, third to the fourth, and fourth to the fifth), we can express the total distance (D) as:
D=4h
Substituting the height of the tetrahedron:
D=4(2√3R)=8√3R
Step 5: Final Expression
Thus, the shortest distance between the first and the fifth layer of the HCP arrangement is:
D=8R√3
Summary
The shortest distance between the first and fifth layers of an HCP arrangement is given by:
D=8R√3
---
In an HCP structure, the layers are arranged in a specific manner. The first layer (A) is followed by the second layer (B), which is then followed by the third layer (A again), the fourth layer (B), and the fifth layer (A). The arrangement alternates between two types of layers.
The distance we are looking for is the vertical distance between the first layer (A) and the fifth layer (A). In HCP, the distance between two consecutive layers can be determined by the height of the tetrahedron formed by the atoms in the layers.
The height (h) of a tetrahedron can be calculated using the formula:
h=2√3R
where R is the radius of the atoms in the structure.
Since the distance between the first layer and the fifth layer involves moving through four heights (from the first layer to the second, second to the third, third to the fourth, and fourth to the fifth), we can express the total distance (D) as:
D=4h
Substituting the height of the tetrahedron:
D=4(2√3R)=8√3R
Thus, the shortest distance between the first and the fifth layer of the HCP arrangement is:
D=8R√3
The shortest distance between the first and fifth layers of an HCP arrangement is given by:
D=8R√3
Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Part-III : Match the column
3 Videos
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-I)
19 Videos
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Exercise -1
24 Videos
- S BLOCK ELEMENTSBOOK - RESONANCECHAPTER - S BLOCK ELEMENTSEXERCISE - INORGANIC CHEMISTRY(s-Block Elements)
36 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCECHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
Knowledge Check
Consider the line L 1 : x 1 y 2 z 1 312 +++ ==, L2 : x2y2z3 123
A0B17√3C413√3D175√3The shortest distance between two Na+ ions in rock - salt arrangement having edge length equal to a√2 picmeters is -
A2aB2a√2Ca√2DaWhat is the nearest distance between two different layers in ABAB arrangement (a=2× radius of the particle)
A√83aB√43aC1√6aD√23a
The shortest distance between line y-x=1 and curve x=y2 is
View SolutionThe shortest distance between the car and the motorcycle if their initial positions are as shown, will be :
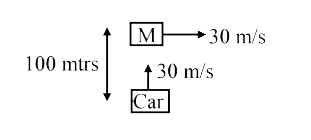
View SolutionIf in a cube of edge of length 6√2 ,then shortest distance between a diagonal and an edge not meeting it, is
View SolutionThe shortest distance between the line x−y=1 and the curve id x2=2y
View SolutionThe length of edge of a cube is a, then shortest distance between the diagonal of cube and an edge skew to it is
View Solution
