A student wants to arrange 4 identical spheres (of radiusR) on a two dimensional floor as close as possible. Finally he could arrange them. Identify the type and dimensions of the figure obtained by joining their centers. Could he occupy the whole available space, if not, then what type of voids were generated. Calculate their number and radius of small ball that can be fitted in them.
The correct Answer is:No, Rhombous: 2R, 60^( º), 120^(º); Triangular voids; 2 voids, 0.155 R
Step by step video, text & image solution for A student wants to arrange 4 identical spheres (of radiusR) on a two dimensional floor as close as possible. Finally he could arrange them. Identify the type and dimensions of the figure obtained by joining their centers. Could he occupy the whole available space, if not, then what type of voids were generated. Calculate their number and radius of small ball that can be fitted in them. by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Part-II : Only one option correct type
42 Videos
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Part-III : Match the column
3 Videos
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Miscellaneous solved problems
16 Videos
- S BLOCK ELEMENTSBOOK - RESONANCECHAPTER - S BLOCK ELEMENTSEXERCISE - INORGANIC CHEMISTRY(s-Block Elements)
36 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCECHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
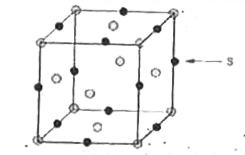
View Solution
Knowledge Check
In hexogonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexongonas and three atoms are sandwiched inbetween them. A space filling model of this structure called haxagonal closed packed (HCP) is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible . Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be 'r'.
The empty space in this HCP unit cell isA0.26B6C12D17In hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space -filling model of this structure, called hexagonal close-packed (HCP), is consituted of a sphere on a flat surface surrouneded in the same plane by six identical spheres as closely possible. Three sphere are then palces over the first layer so that they touch each other and represent second layer is covered with third layer that is identical to the bottom layer in relative position. Assume radius of enery sphere to be r.
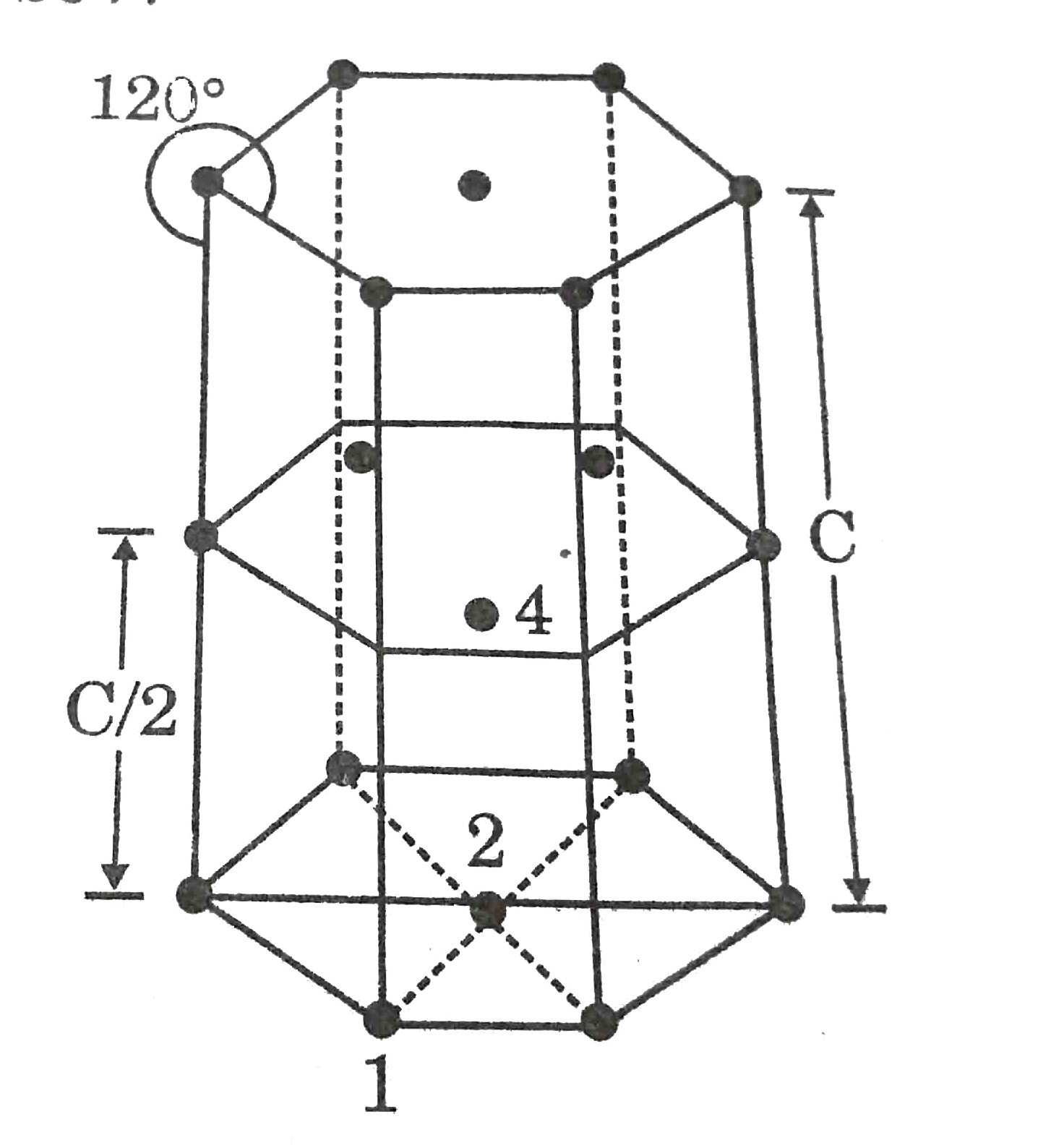
The number of atoms in the HPC unit cell is :A4B6C12D17In hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagon and three atoms are sandwiched in between them. A space filling model of this structure, called hexagonal close packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical sphere as closely as possible. Three spheres are then placed over the first layer so that they touch other and represent the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be same
The number of atoms in this HCP unit cell isA4B6C12D17
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the spinel structure, oxide ions are cubic close packed whereas 1/8th of tetrahedral voids are occupied by A2+ cations and 1/2 of octahedral voids are occupied by B3+ cations. The general formula of the compound having spinel structure is
View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
View SolutionTwo dimensional close packed structure can be generated by stacking the rows of close packed spheres. This can be done in two different ways.
(I) The second row may be placed in contact with the first one, such that the spheres of the second row are exactly above those of first row. The spheres of the two rows are aligned vertically as well as horizontally.
If we call the first row as 'A' type of row, the second row being exactly same as the first one is also of 'A' type. Similarly, we may place more rows to obtain AAAA.... type arrangement
(II) In this type, the second row may be placed above the first one in a staggered manner such that its spheres. fit in depressions of first row. if the arrangement of spheres in the first row is called 'A' type the one in the second row is different and may be called 'B' type. When the third row is placed adjacent to the second in staggered manner, its spheres are aligned with those of first layer. Hence this layer is also 'A' type. The spheres of similarly placed fourth row will be aligned with those of the second row ('B' type). Hence this arrangement is of ABAB.... type
Of type (I) & type (II), the packing efficiency
View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism.Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them.A space-fitting model of this structure, called hexagonal closed-packed (HCP), is constitution of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible Three spheres are then placed over the first layer so that they touch each other and represent the second layer.Each one of these three spheres touches three spheres of the bottom layer.Finally, the second layer is covered with third layer that is identical to the bottom layer in relative position.Assume radius of even sphere to be 'r'.
The volume of this HCP unit cell is :
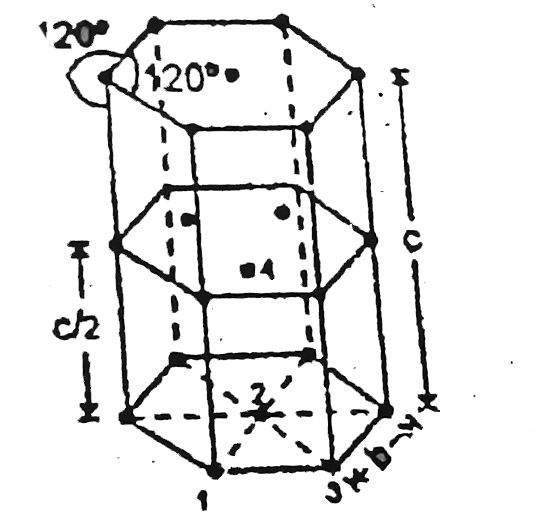
View SolutionIn hexagonal systems of crystals, a frequently ecounted arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are reqular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. There spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three sphere touches three spheres of the bottom layer. Finally the second layer is covered with third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be 'r'

The number of atoms in the HCP unit cell is
View Solution
