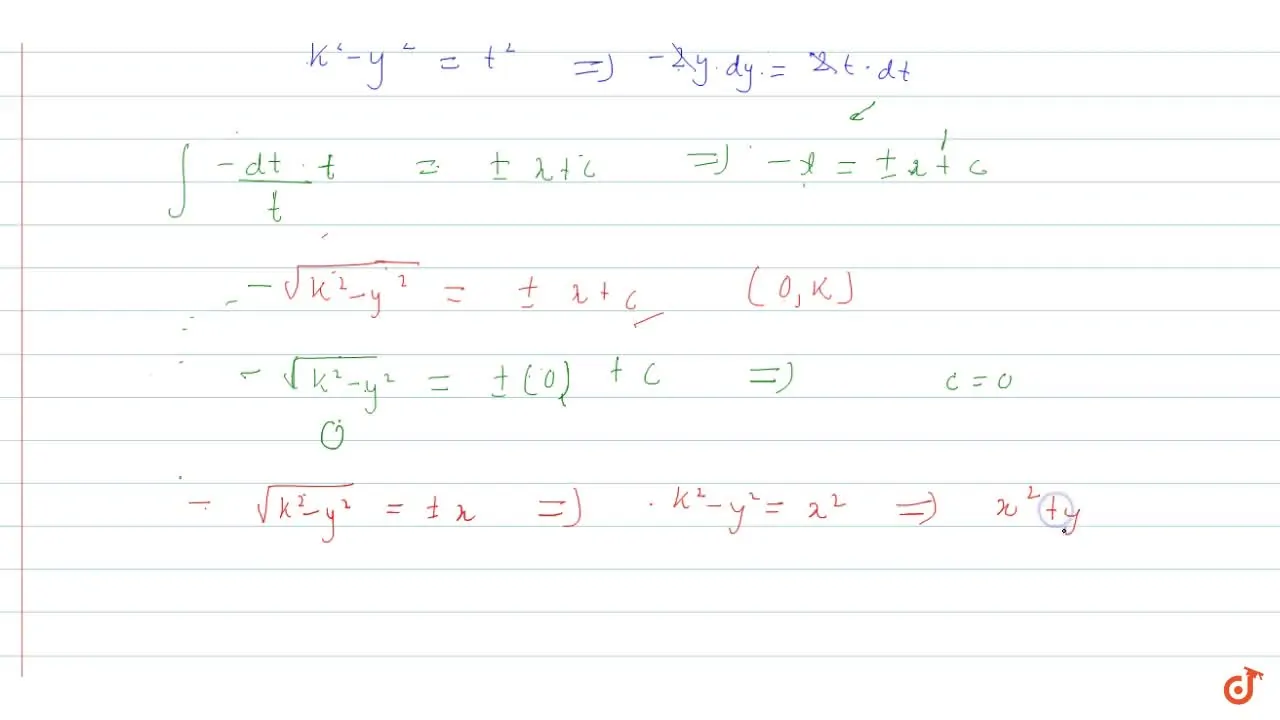A normal is drawn at a point P(x,y) of a curve. It meets the x-axis at Q. If PQ has constant length k, then show that the differential equation describing such curves is ydydx=±√k2−y2 . Find the equation of such a curve passing through (0,k).
The equation of normal to required curve at P(x,y) is given by (X−x)+dydx(Y−y)=0
For point Q, where is this normal meets X-axis, put Y=0. then X=x+ydydx
∴Q=(x+ydydx,0)

According to question, length of PQ=k.
or (ydydx)2+y2=k2
or ydydx=±√k2−y2
Which is the required differential equation of given curve.
Solving this, we get
∫ydx√k2−y2=∫±dx
or −122√k2−y2=±x+C
or −√k2−y2=±x+C
As it passes through (0,k), we get C=0
Thus, equation of curve is −√k2−y2=+x
or x2+y2=k2
Similar Questions
A normal is drawn at a point P(x,y) of a curve. It meets the x-axis at Q. If PQ has constant length k, then show that the differential equation describing such curves is ydydx=±√k2−y2 . Find the equation of such a curve passing through (0,k).
View SolutionA normal is drawn at a point P (x, y) of a curve. It meets the X- axis at Q. If PQ is of constant length k, then the differential equation describing such a curve is
View SolutionA normal is drawn at a point P(x,y) of a curve. It meets the X-axis at Q. If PQ is of constant length k, then the differential equation describing such a curve is
View SolutionA normal is drawn at a point P(x, y) of a curve lt meets the x-axis at Q lf PQ is of constant length k such a curve passing through (0,k) is
View SolutionA normal is drawn at a point P(x,y) of a curve. It meets the x-axis at Q such that PQ is of constant length k. Answer the question:The differential equation describing such a curve is (A) ydydx=±√k2−x2 (B) xdydx=±√k2−x2 (C) ydydx=±√k2−y2 (D) xdydx=±√k2−y2
View SolutionThe differential equation of the family of curves y=P(x+Q)2 is
View SolutionTangent drawn at any point P on a curve meets x-axis at Q such that circumcentre of ΔPOQ has abscissa half that of ordinate. The differential equation to such a curve is
View SolutionFor the differential equation xydydx=(x+2)(y+2), find the solution curve passing through the point (1,−1).
View SolutionFor the differential equation :
xydydx=(x+2)(y+2),
find the solution of curve passing through the point (1, -1).View SolutionA normal is drawn at a point P(x,y) on a curve. It meets the x-axis and thedus ofthe director such that (x intercept)−1 + (y-intercept)−1=1, where O is origin, the curve passing through (3,3).
View Solution