If set A ={x∣x2(x−5)(2x−1)(5x+1)(x+2)<0} and
Set B={x∣3x+16x3+x2−x>0} then A∩B does not contain
A
(1,4)
B
(5,11)
C
(−32,−12)
D
None of these
Video Solution
Text Solution
The correct Answer is:B
we have x2(x−5)(2x−1)(5x+1)(x+2)<0 ltbgt 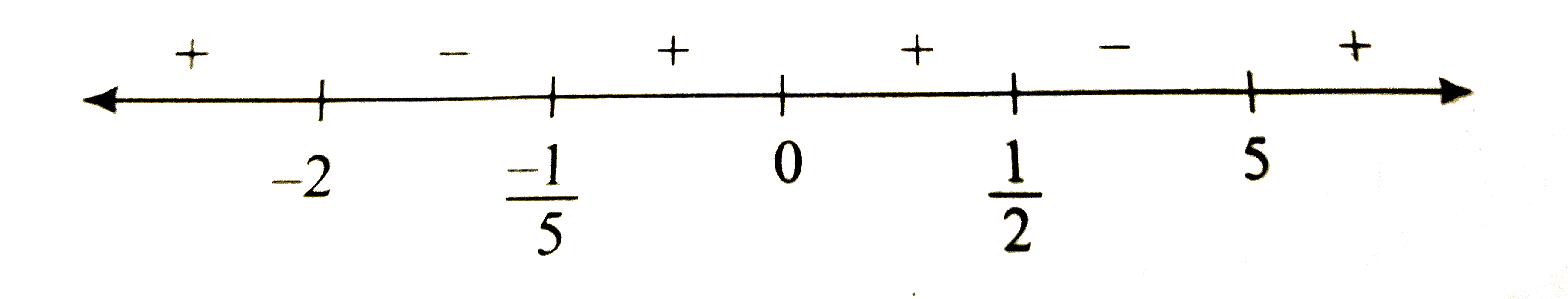
from the sign scheme , solution is (−2,−15)∪(15,5)
Now 3x+16x3+x2−x>0
⇒3x+1x(3x−1)(2x+1)>0
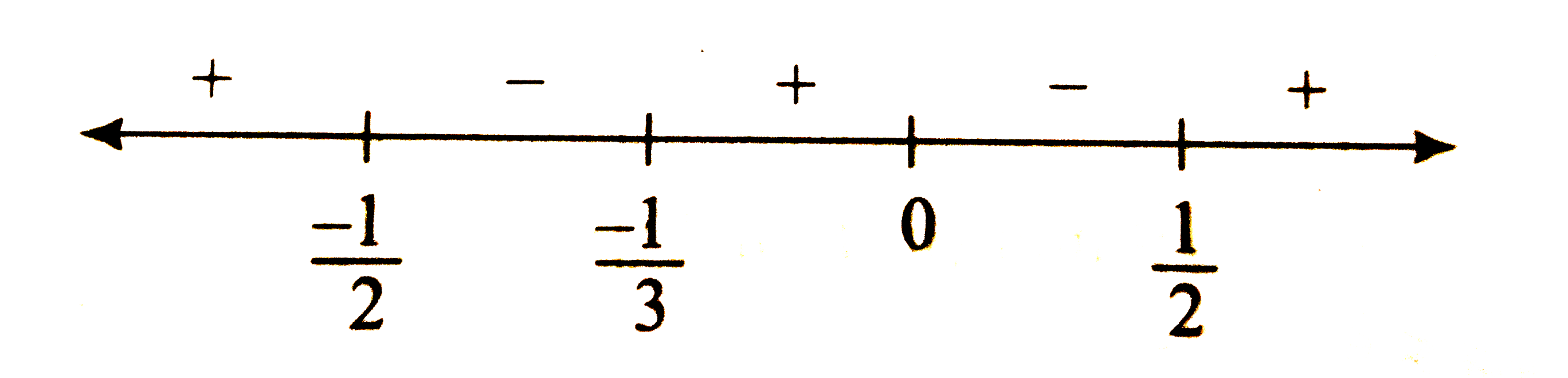
form the sign scheme solution is
(−∞,−12)∪(−13,0)∪(13,∞)
Clearly from (i) and (ii) options ( s) (1) and ( 3) and correct
|
Topper's Solved these Questions
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archieves
1 Video
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Exercise 1.5
12 Videos
- SEQUENCE AND SERIESBOOK - CENGAGECHAPTER - SEQUENCE AND SERIESEXERCISE - Question Bank
36 Videos
- SETS AND RELATIONSBOOK - CENGAGECHAPTER - SETS AND RELATIONSEXERCISE - Question Bank
15 Videos
Similar Questions
Knowledge Check
If 6x(2x2+5x−2)=1,x>0, then the value of x3+1x3 is :
AA)38√17BB)5√178CC)5√1716DD)34√17The solution set of (x2+x+1)(x2)log(x)(x+1)(x+9)<0 is
A(0,1)∪(1,2)B(1,2)C(0,1)D(0,2)If x2+6x−27>0andx2−3x−4<0 , then :
Ax>3B−1<x<4C3<x<4Dx<−9orx>−1
(x+3)(x2−5x+6)(x2+x+1)(x−4)≤0
View SolutionIf x2−5x+6x2+x+1<0 then x belong to
View SolutionIf x2+6x−27>0andx2−3x−4<0 , then :
View SolutionIf 2x+13x=5, the value of 5x6x2+20x+1 is
View SolutionIf universal set U={x∣x5−6x4+11x3−6x2=0}
A={x∣x2−5x+6=0} and B={x∣x2−3x+2=0} Then, (A∩B) is equal to
View Solution
