Out of 100 students, 15 passed in English, 12 passed in Mathmatics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science , 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science.
(ii) in Mathematics and Science but not in English.
(iii) in Mathematics only.
(iv) in more than one subject only.
Video Solution
Text Solution
The correct Answer is:(a) 2 (b) 3 ( c) 3 (d) 9
Let M be the set of students who passed in Mathematics , E be the set of students who passed in English and S be the set of students who passed in Science
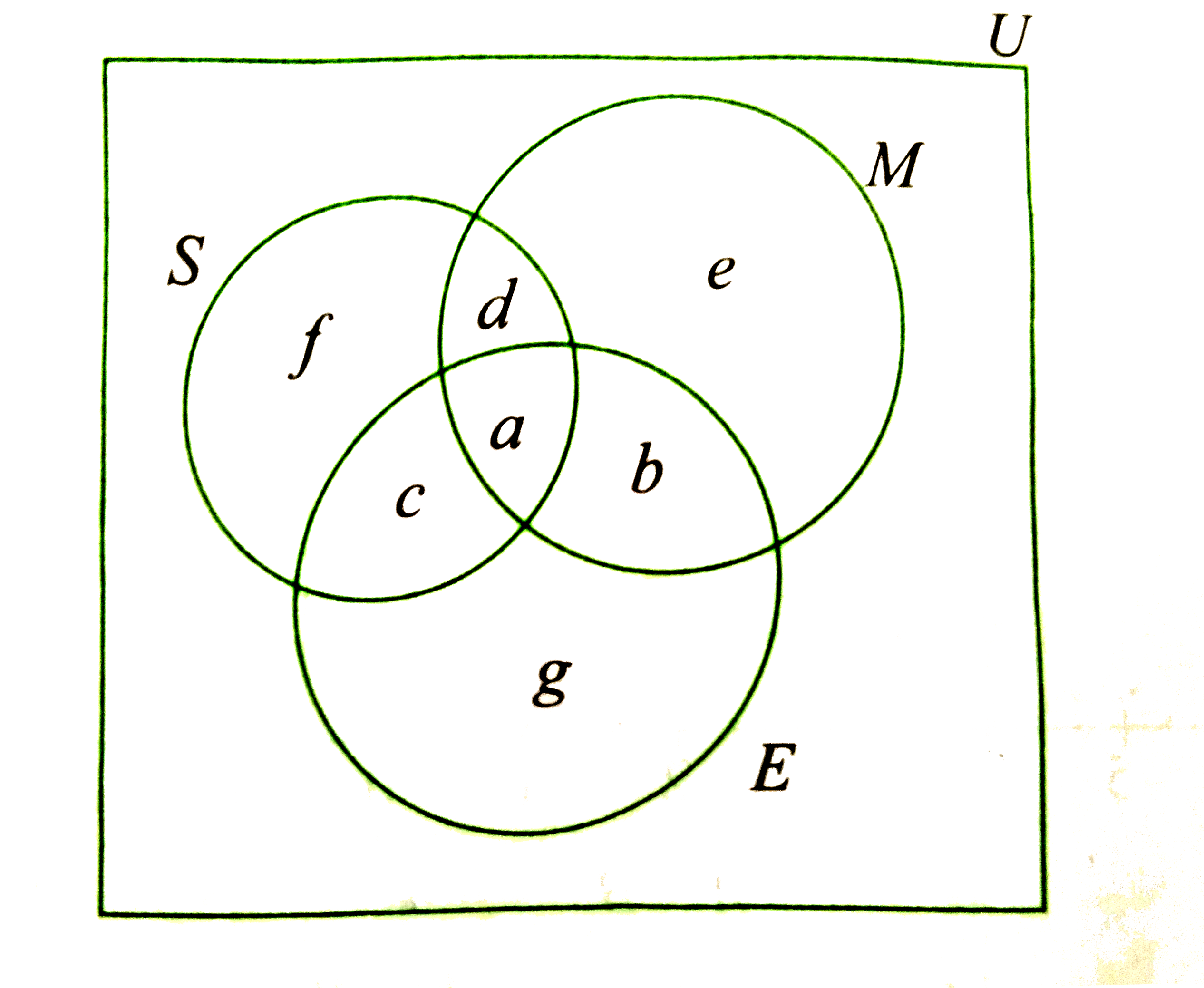
Given n( U)= 100
n( E) = 15 , n( M ) = 12 , n(s) = 8
n(E∩M)=6,n(M∩S)=7
n(E∩S)=4andn(E∩M∩S)=4
From the Venn diagram , we have
a=(E∩M∩S)=4anda+d=n(M∩S)=7⇒d=3
a+b=n(M∩E)=6 ⇒b=2
a+c=n(S∩E)=4 ⇒c=0
a+b+ d+ e= n( M)= 12
⇒4+2+3+e=12 ⇒e=3
a+b+c+g = 15
⇒4+2+0+g=n(E)=15⇒g=9
a+c+d+f= n(s)=8
⇒4+0+3+f=8 ⇒f=1
Number of students passed in
(a) English and Mathematics but not in Science = b= 2
( b) Mathematics and Science but not in English = d= 3
Mathmatics only = e= 3
( d) more than one subject =a+b+c+d+= 4+2+0+3=9
|
Topper's Solved these Questions
- SET THEORY AND REAL NUMBER SYSTEM Book:CENGAGEChapter:SET THEORY AND REAL NUMBER SYSTEM Exercise:Exercise 1.2
Explore 8 Videos
- SET THEORY AND REAL NUMBER SYSTEM Book:CENGAGEChapter:SET THEORY AND REAL NUMBER SYSTEM Exercise:Exercise 1.3
Explore 13 Videos
- SET THEORY AND REAL NUMBER SYSTEM Book:CENGAGEChapter:SET THEORY AND REAL NUMBER SYSTEM Exercise:Archieves
Explore 1 Video
- SEQUENCE AND SERIESBook:CENGAGEChapter:SEQUENCE AND SERIESExercise:Question Bank
Explore 36 Videos
- SETS AND RELATIONSBook:CENGAGEChapter:SETS AND RELATIONSExercise:Question Bank
Explore 15 Videos
Similar Questions
Knowledge Check
Mathematics : Logic : : Science : ?
AExperimentBLaboratoryCScientistDFactsMathematics is the science of
AintellectualBnumbersCcalculationDall the aboveMathematics is the science of
AIntellectualBNumbersCCalculationsDAll the above
Mathematics is the science of
View SolutionMathematics is the science of
View SolutionThe main aim to conduct Mathematics and Science Olympiads is to
View SolutionIn an examination out of 100 students, 75 passed in English 60 passed in Mathematics and 45 passed in both English and Mathematics. What is the number of students passed in exactly one of the two subjects?
View SolutionWho said "Mathematics is the gateway and key of all sciences."
View Solution

