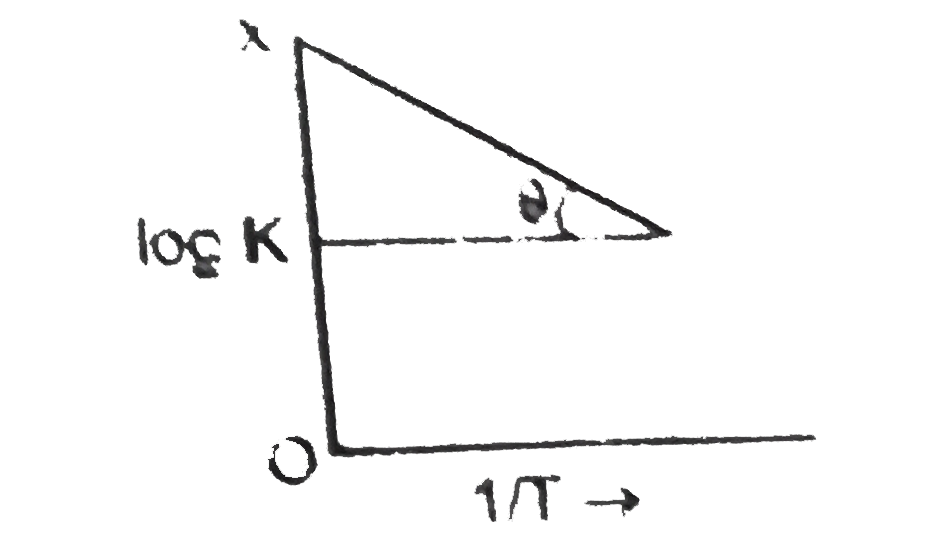
Variation of equiibrium constant K with temperature T is given by van 't Holf equation,
logK=logA−ΔH∘2.303RT
A graph between log K and T−1 was a straight line as shown in the figure and having θ=tan−1(0.5)andOP=10. Calculate:
(a) ΔH∘ (standard heat of reaction)when T=300K,
(b) A (pre-exponetial factor),
(c) Equilibrium constant K at 300K,
(d) Kat900KifΔH∘ is independent of temperature.
The correct Answer is:(a) 9.574Jmol−1; (b)A=1010; (c) 9.96×109; (d)9.98×109
(a) log10K=log10A−ΔH∘2.303RT
It is an equation of a straight line of the type y=c+mx
Slope 'm'=tan0=ΔH∘2.303R
0.5=ΔH∘2.303×8.314
ΔH∘=9.574Jmol−1
(b) Intercept,C'=log10A=10 A=1010
(c) logK=10−9.5742.303×8.314×298
K=9.96×109
(d) log(K2K1)=ΔH2.303R{1T1−1T2}
log(K2)9.96×109=9.5742.303×8.314{1298−1798}
On solving K2=9.98×109
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:(MSPs)
Explore 8 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Board Level Exercise
Explore 33 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Advanced Level Problems (Part-3)(Stage-5)
Explore 2 Videos
- CHEMICAL BONDINGBook:RESONANCEChapter:CHEMICAL BONDINGExercise:Inorganic chemistry (Chemistry Bonding)
Explore 49 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Book:RESONANCEChapter:D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Exercise:Match the column
Explore 1 Video
Similar Questions
Knowledge Check
For a hypothetical reaction: A(g)+B(g)⇔C(g)+D(g) a graph between log Keq and T− is striaght line as follows, where θ=tan−10.5 and OA=1.0 (S.I. units) Assuming ΔH∘ is independent of temperature, the equilibrium constant at 298 K will be:
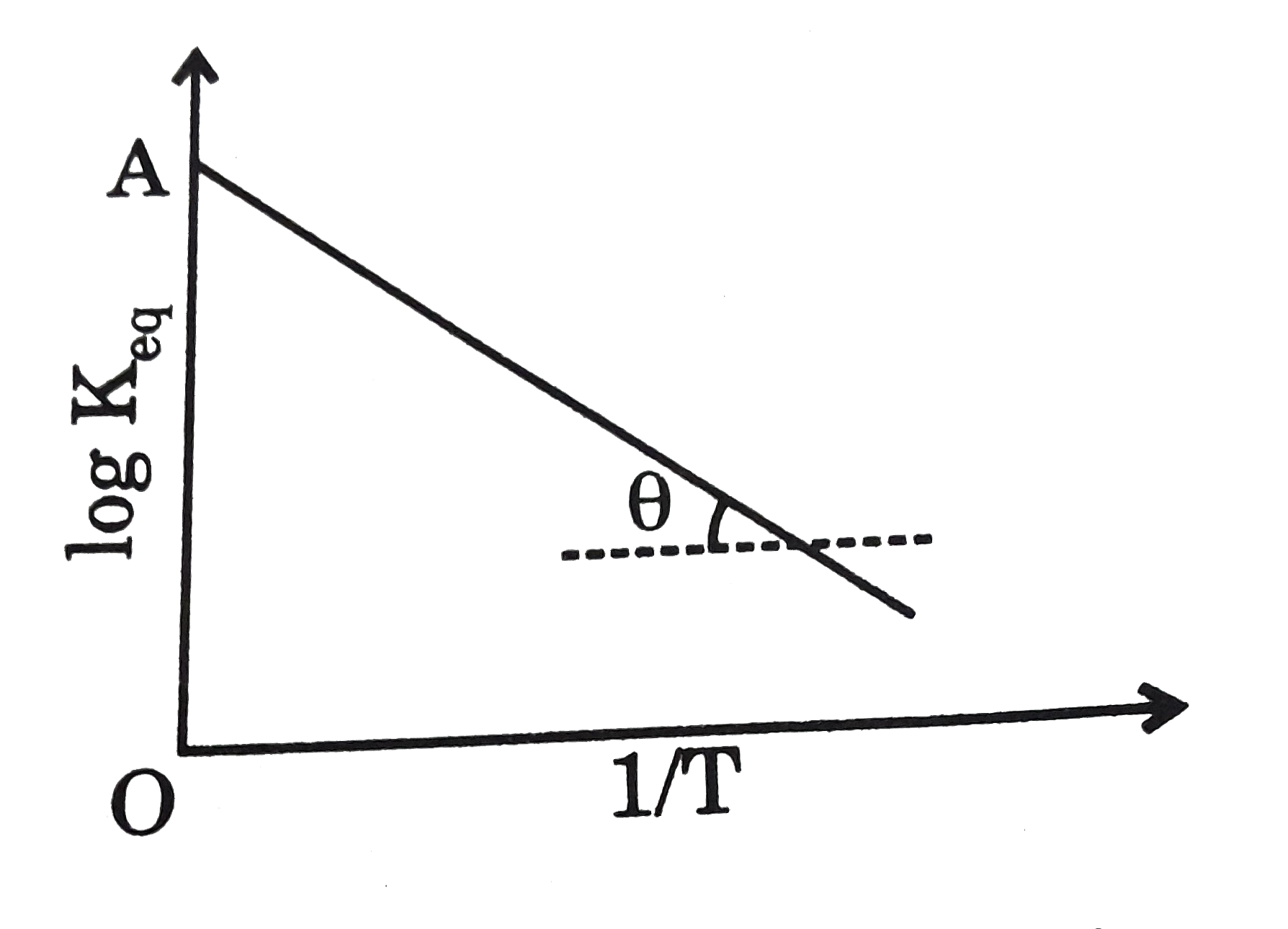 A10.002×109B3.79×108C7.96×109D9.96×109
A10.002×109B3.79×108C7.96×109D9.96×109Rate constant k of a reaction varies with temperature according to the equation, log k = constant -Ea2.303RT When a graph is plotted for logk versus 1/T a straight line with a slope -5632 is obtained. The energy of activation for this reaction is
A127.67 kJ mol−1B107.84 kJ mol−1C86 kJ mol−1D246.8 kJ mol−1Rate constant k varies with temperature by equation, log k (min+−1)=5−2000T(K) We can conclud:
Apre-exponential factor A is 5BEa is 2000 kcalCpre-exponential factor A is 105DEa is 9.212 kcal
A graph plotted between log10Kc and 1/T is straight line with intercept 10 and slpoe equal t0 0.5. Calculate :
(i) pre -exponential factor A.
(ii) heat of reaction at 298K.
(iii) equilibrium constant at 298K.
(iv) equilibrium constant in at 800k assuming ΔH remains constant in between 298K and 800K.
View SolutionThe rate constant 'k'. For a reaction varies with temperature 'T' according to the question. logk=logA−Ea2.303R(1T)
Where Ea is the activation energy. When a graph is plotted for logkvs1/T, a straight line with a slope of −4250 K is obtained. Calcualte Ea for this reaction.
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
Select the correct statement :
View SolutionThe variation of rate constant with temperature is given by the integrated from of the Arrhenius equation, log10k=−Ea2.303RT + constant
where k = rate cosntant and Ea is the experimental activation energy. If for a certain reaction, log10k=−3163.0T+11.899, calculate Ea.
View SolutionGraph between logk and 1/T [k rate constant (s−1) and T and the temperature (K)] is a straight line with OX=5,θ=tan−1(1/2.303). Hence −Ea will be

View Solution