Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
To solve the problem of drawing a circle and two lines parallel to a given line such that one is a tangent and the other is a secant to the circle, follow these steps:
1. Draw a Circle:
- Start by drawing a circle using a compass. Choose a center point (let's call it O) and draw a circle with a suitable radius.
2. Draw a Given Line:
- Next, draw a straight line (let's call it AB) on your paper. This line will serve as the reference for the parallel lines you will draw.
3. Determine the Position of the Tangent Line:
- To draw a tangent line parallel to line AB, you need to find a point on the circle. Choose a point on the circumference of the circle (let's call it P).
4. Draw the Tangent Line:
- From point P, draw a line (let's call it PQ) that is parallel to line AB. This line will be the tangent to the circle at point P. Ensure that it only touches the circle at point P.
5. Determine the Position of the Secant Line:
- Now, you need to draw a secant line. Choose a point outside the circle (let's call it Q) such that when you draw a line through Q, it intersects the circle at two points.
6. Draw the Secant Line:
- Draw a line (let's call it CD) that passes through point Q and intersects the circle at two points (let's call them C and D). This line will be the secant to the circle.
7. Verify Parallelism:
- Ensure that both lines PQ (the tangent) and CD (the secant) are parallel to the original line AB.
Final Diagram:
- You should now have a circle with:
- A tangent line PQ that touches the circle at point P.
- A secant line CD that intersects the circle at points C and D.
- Both lines PQ and CD are parallel to the given line AB.
- Start by drawing a circle using a compass. Choose a center point (let's call it O) and draw a circle with a suitable radius.
- Next, draw a straight line (let's call it AB) on your paper. This line will serve as the reference for the parallel lines you will draw.
- To draw a tangent line parallel to line AB, you need to find a point on the circle. Choose a point on the circumference of the circle (let's call it P).
- From point P, draw a line (let's call it PQ) that is parallel to line AB. This line will be the tangent to the circle at point P. Ensure that it only touches the circle at point P.
- Now, you need to draw a secant line. Choose a point outside the circle (let's call it Q) such that when you draw a line through Q, it intersects the circle at two points.
- Draw a line (let's call it CD) that passes through point Q and intersects the circle at two points (let's call them C and D). This line will be the secant to the circle.
- Ensure that both lines PQ (the tangent) and CD (the secant) are parallel to the original line AB.
- You should now have a circle with:
- A tangent line PQ that touches the circle at point P.
- A secant line CD that intersects the circle at points C and D.
- Both lines PQ and CD are parallel to the given line AB.
Similar Questions
Draw a line parallel to a given line.
View SolutionSecant of a circle
View SolutionTwo lines parallel to the same line are ___ to each other .
View Solutionprove that two lines m and n be parallel to the same given line are parallel to each other.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
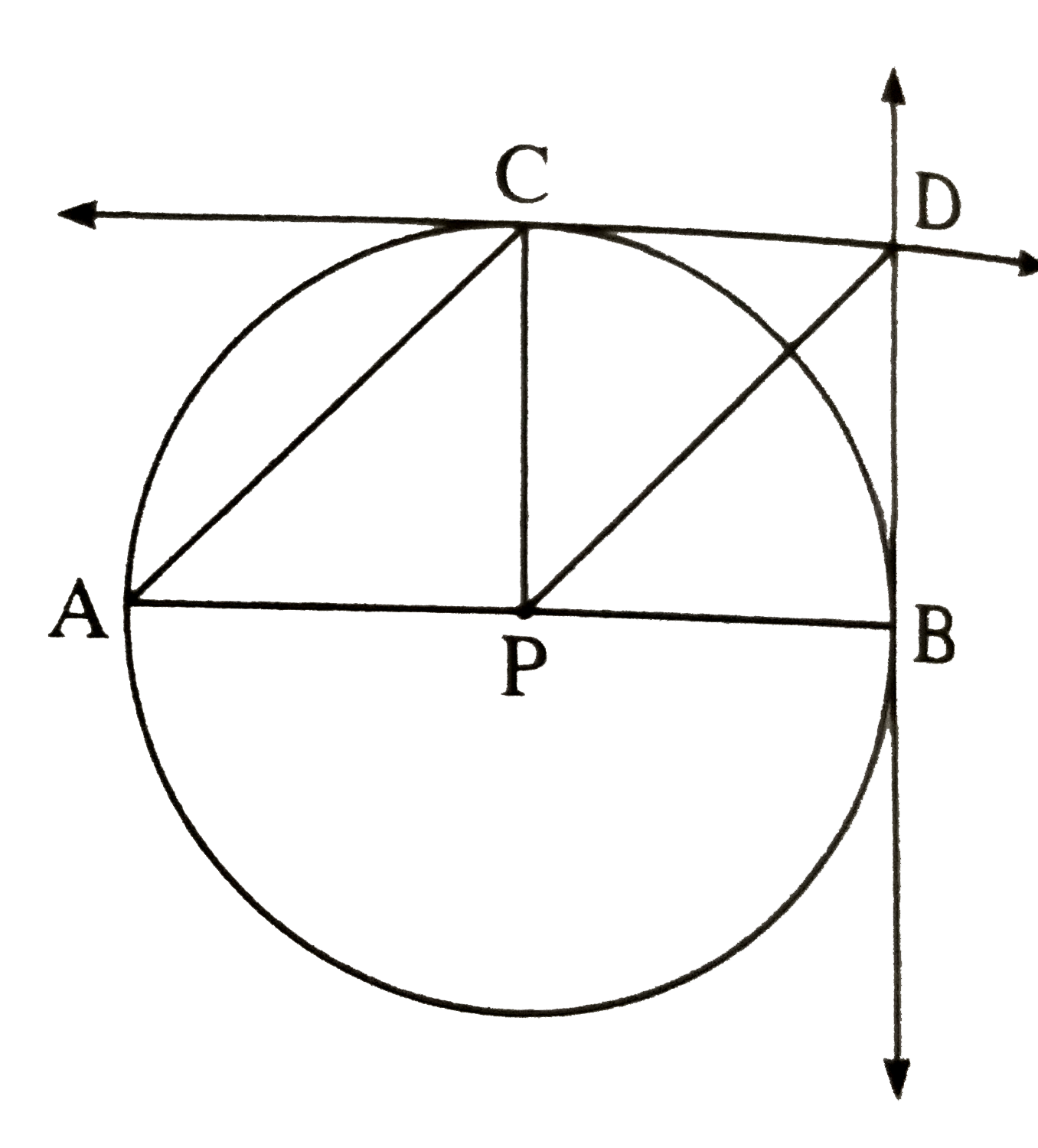
View SolutionFill in the blanks
(i) A line intersecting a circle in two distinct points is caled a….
(ii) A circle can have… parallel tangents at the most.
(iii) The common point of a tangent to a circle and the circle is called the….
(iv) A circle can have.... tangents.
View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

View SolutionDraw a circle of radius 2.6 cm. Draw a tangent to the circle from any point on the circle.
View SolutionDraw a line segment XY as the diameter of a circle .
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.
View Solution
