An electric sander has a continuous belt that rubs against a wooden surface as shown schematically in figure. The sander is 40% percent efficient and drawns a power of 1200 W. The belt speed is . If the sander is pushing against the wood with a normal force of 100 Newton, the coefficient of friction is , which is ?
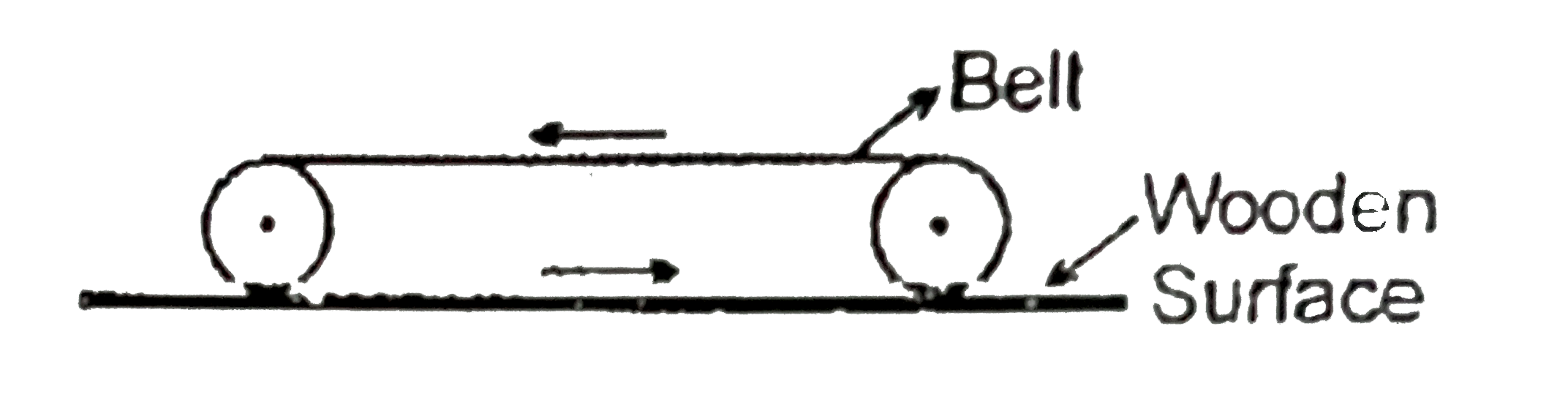
The correct Answer is:1

For 2M
For M :
Topper's Solved these Questions
Similar Questions
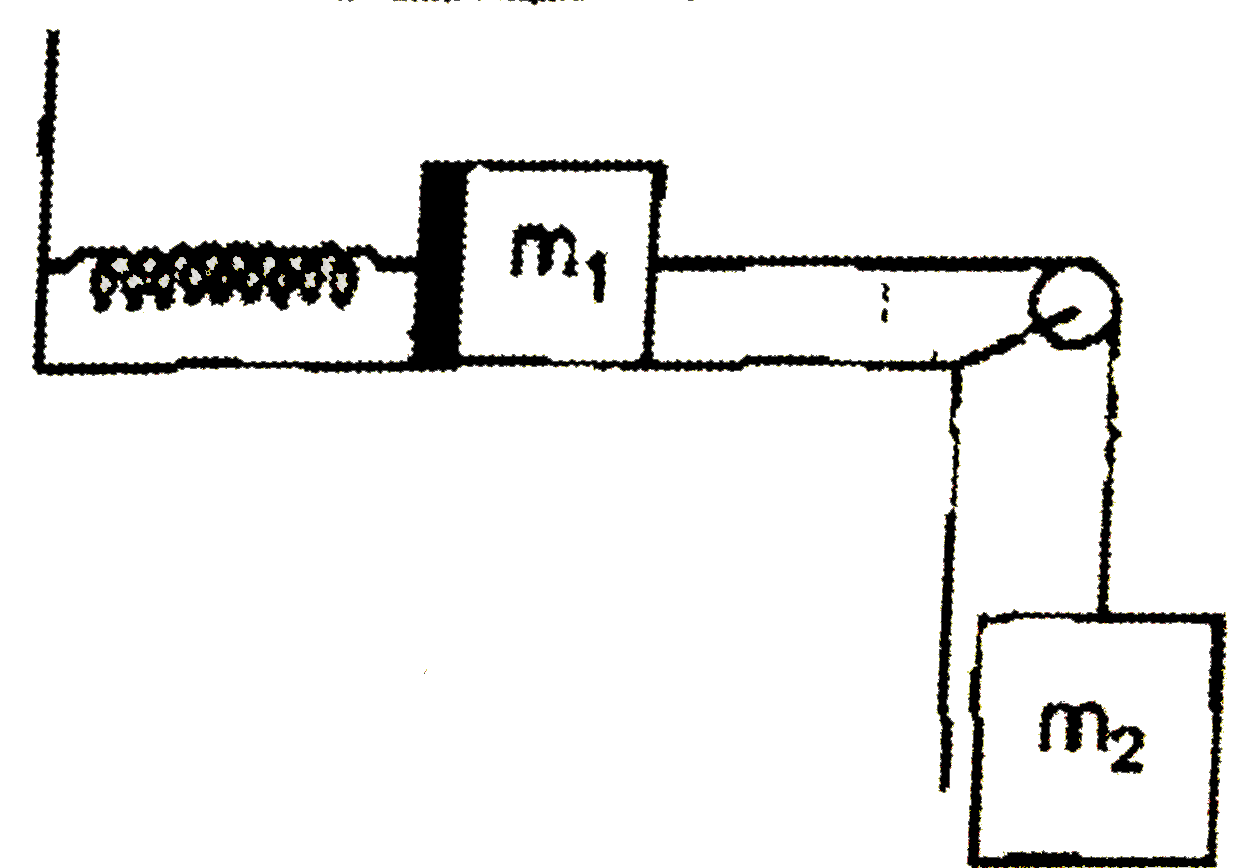
In Fig 3E.17, the mass m2 rests on a rough table. The mass m1 is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is μk.
(a) Find the speed of the blocks after the spring is released and m2 has fallen a distance of h.
(b) If the spring is attached to the block and it falls a distance h before coming to rest, calculate the coefficient of friction μk.
View Solution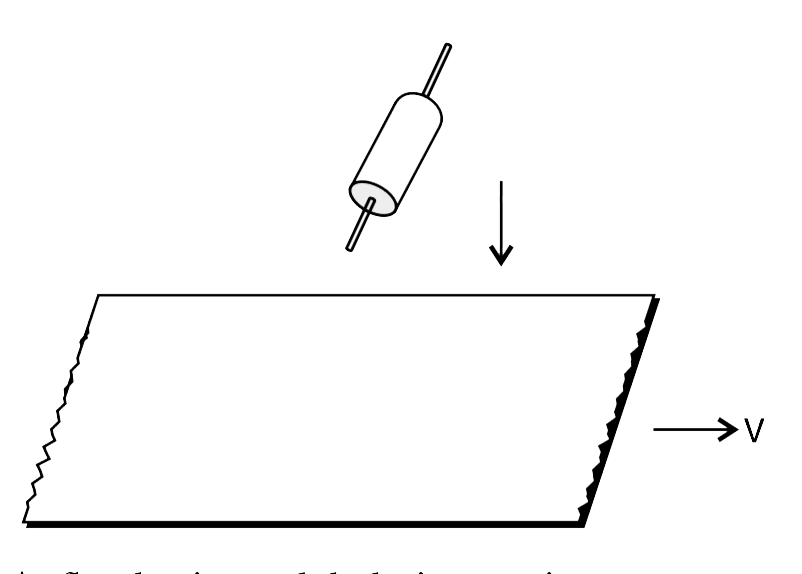
A flat horizontal belt is running at a constant speed V. There is a uniform solid cylinder of mass M which can rotate freely about an axle passing through its centre and parallel to its length. Holding the axle parallel to the width of the belt, the cylinder is lowered on to the belt. The cylinder begins to rotate about its axle and eventually stops slipping. The cylinder is, however, not allowed to move forward by keeping its axle fixed. Assume that the moment of inertia of the cylinder about its axle is 12MR2 where M is its mass and R its radius and also assume that the belt continues to move at constant speed. No vertical force is applied on the axle of the cylinder while holding it.
(a) Calculate the extra power that the motor driving the belt has to spend while the cylinder gains rotational speed. Assume coefficient of friction =μ.
(b) Prove that 50% of the extra work done by the motor after the cylinder is placed over it, is dissipated as heat due to friction between the belt and the cylinder
View Solution
Knowledge Check
A very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity ω. The wall of funnel makes an angle 37∘ with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is μ (Take g=10m/s2)

The friction force acting between the block and surface (if μ=0.3) of funnel at ω=5rad/s is :A6.6 NB4 NC2.2 NDzeroA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity ω. The wall of funnel makes an angle 37∘ with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is μ (Take g=10m/s2)

The maximum value of angular velocity for which no relative slipping occur and also direction of frictional force is : (take μ=2/3)A√4253 rad/sec, down the surface of funnelB√253 rad/sec, up the surface of funnelC√259 rad/sec, up the surface of funnelD√259 rad/sec, down the surface of funnelA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity ω. The wall of funnel makes an angle 37∘ with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is μ (Take g=10m/s2)
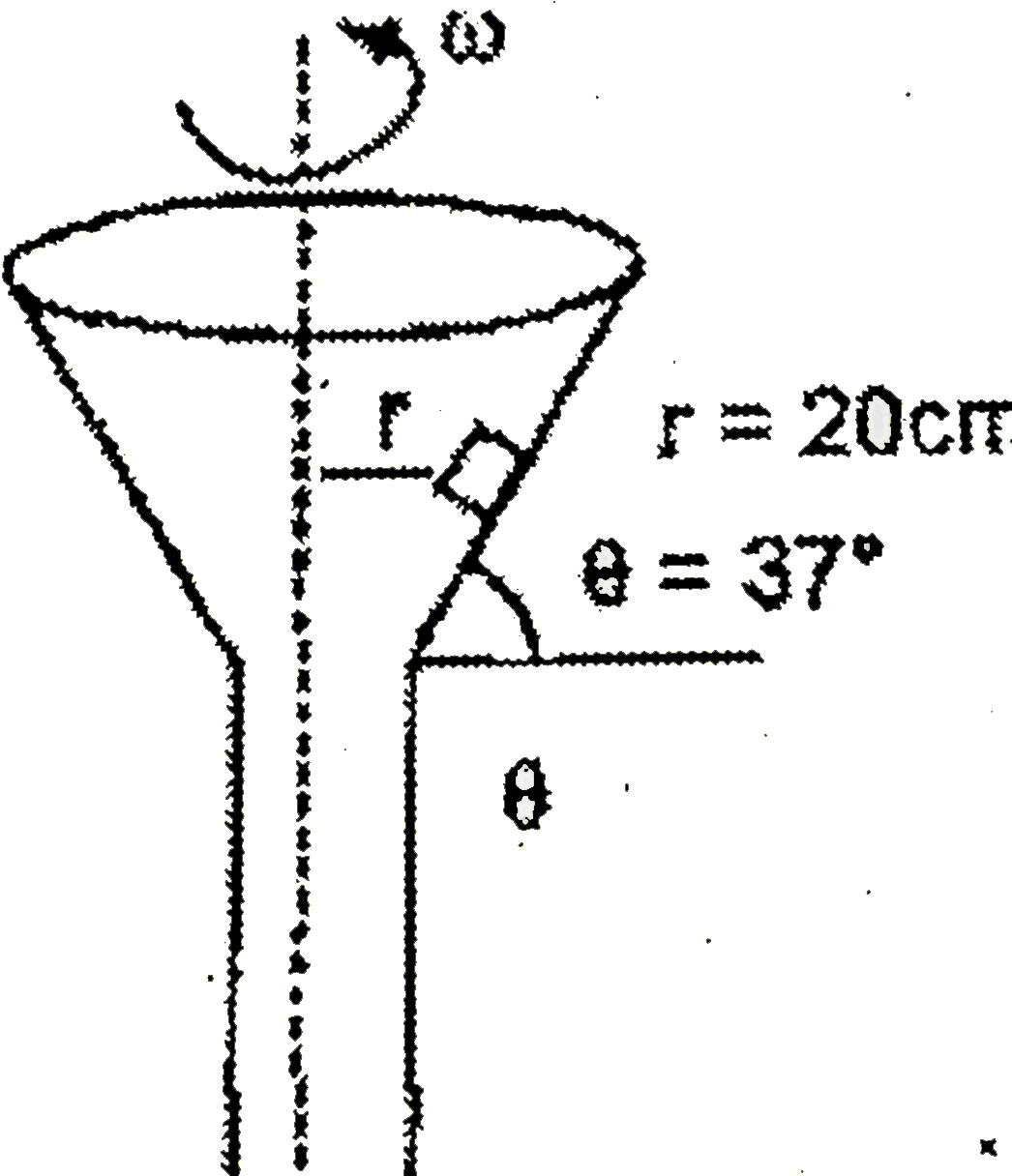
The mimimum value of angular velocity for which relative slipping occurs and also the direction of frictional force acting μ=2/3 :A√259B√153C√925D√325
A block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View Solution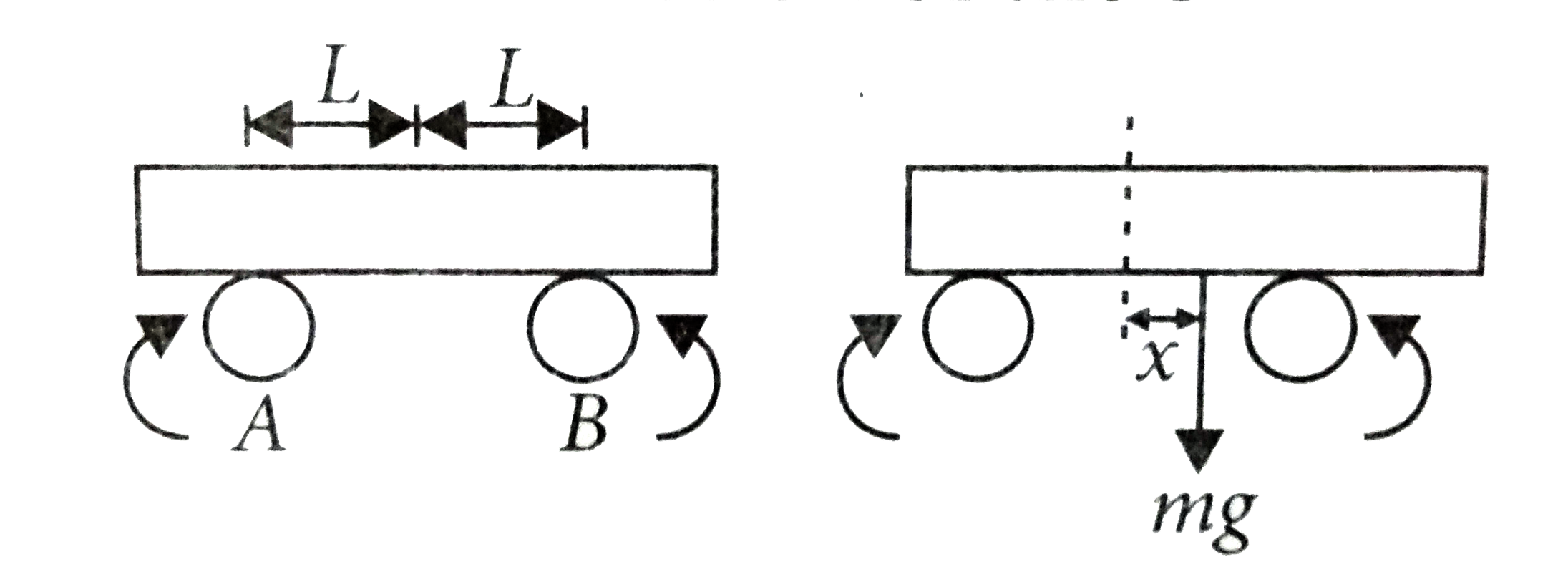
A uniform bar with mass m lies symmetrically across two rapidly rotating fixed rollers, A and B with distance L=2.0 cm between the bar's centre of mass and each roller. The rollers, whose directions of rotation are shown in figures slip against the bar with coefficient of kinetic friction μk=0.40. suppose the bar is displaced horizontally by the distance x as shown in figure and then released. the angular frequency ω of the resulting horizontal simple harmonic motion of the bar is (in rad s−1)
View SolutionTwo blocks A and B of masses 2kg and 4kg are placed one over the other as shown in figure. Atime varying horizontal force F=2t is applied on the upper block as shown in figure. Here t is in second and F is in newton. Drow a graph showing acceleration of A and B on y-axis and time on x-axis.Coefficient of friction between A and B is μ=12 and the horizontal surface over which B is placed smooth. (g=10m/s2)

View SolutionA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity ω. The wall of funnel makes an angle 37∘ with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is μ (Take g=10m/s2)

For what value of ω, there would be no frictional force acting between the surfaces :
View SolutionA block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30∘ by a force of 10 N parallel to the inclined surface as shown in the figure.
The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, then the work against gravity is (Take g=10ms−2)
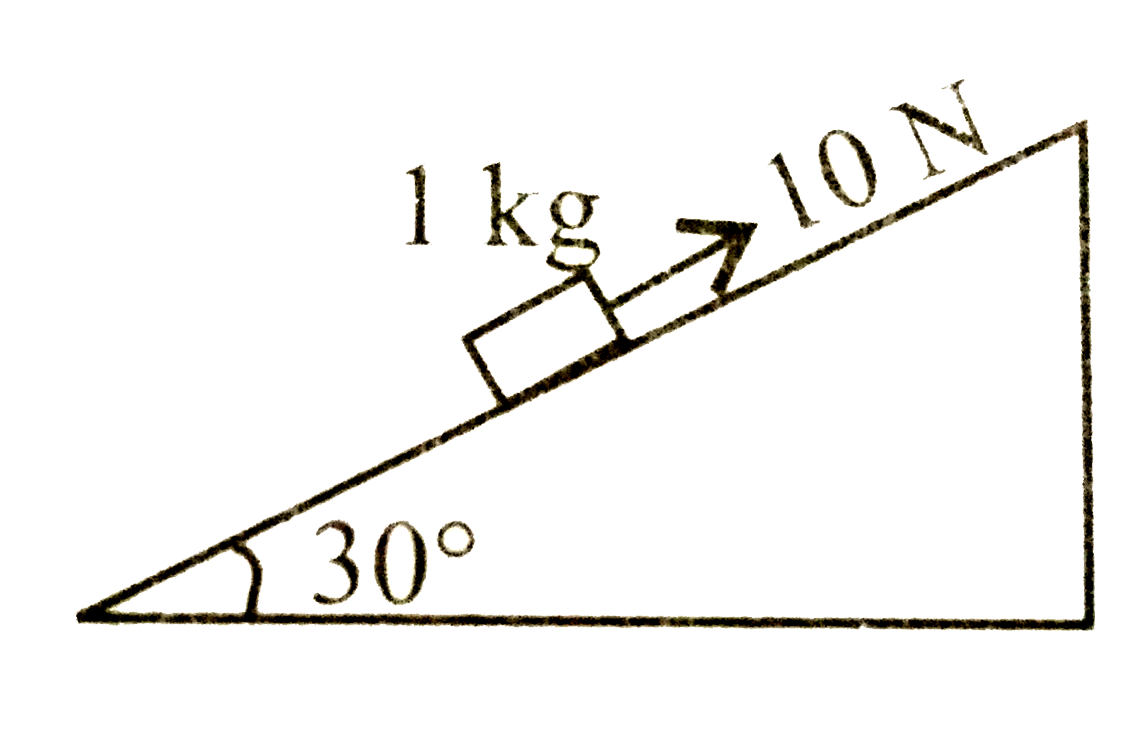
View Solution

