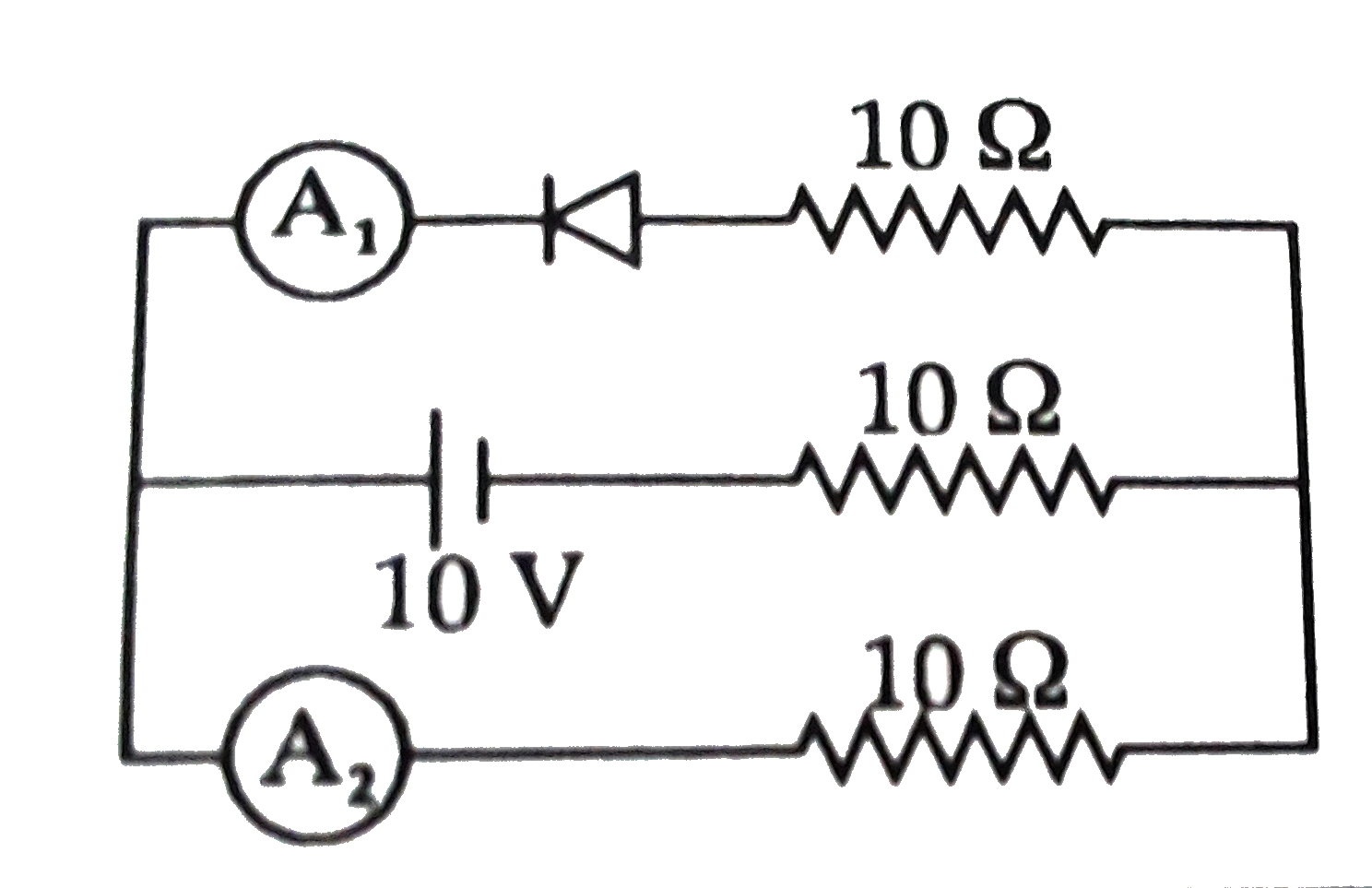
In the figure, the blocks A,B and C of mass m each have accelerations a1,a2 and a3 respectively. F1 and F2 are external forces of magnitude 2mg and mg respectively.
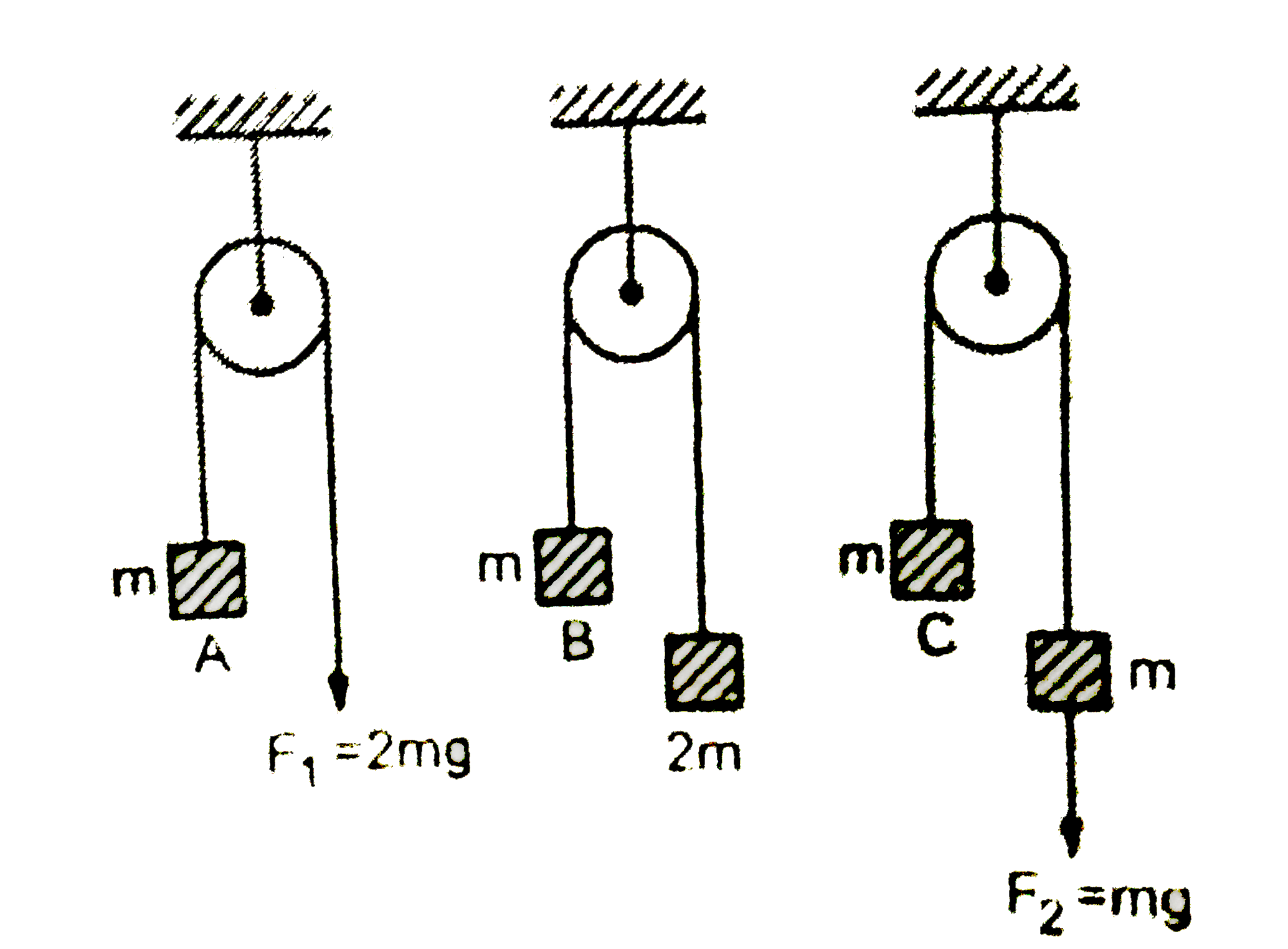
a1=a2=a3
a1>a3>a2
a1=a2,a2>a3
a1>a2,a2=a3
The correct Answer is:D
Extension in the spring is
x=AB−R=2Rcos30∘−R=(√3−1)R
∴ Spring force
F=kx=(√3+1)mgR(√3−1)R=2mg
Free body diagram of bead is shown in figure.
N=(F+mg)cos30∘=(2mg+mg)√32=3√3mg2
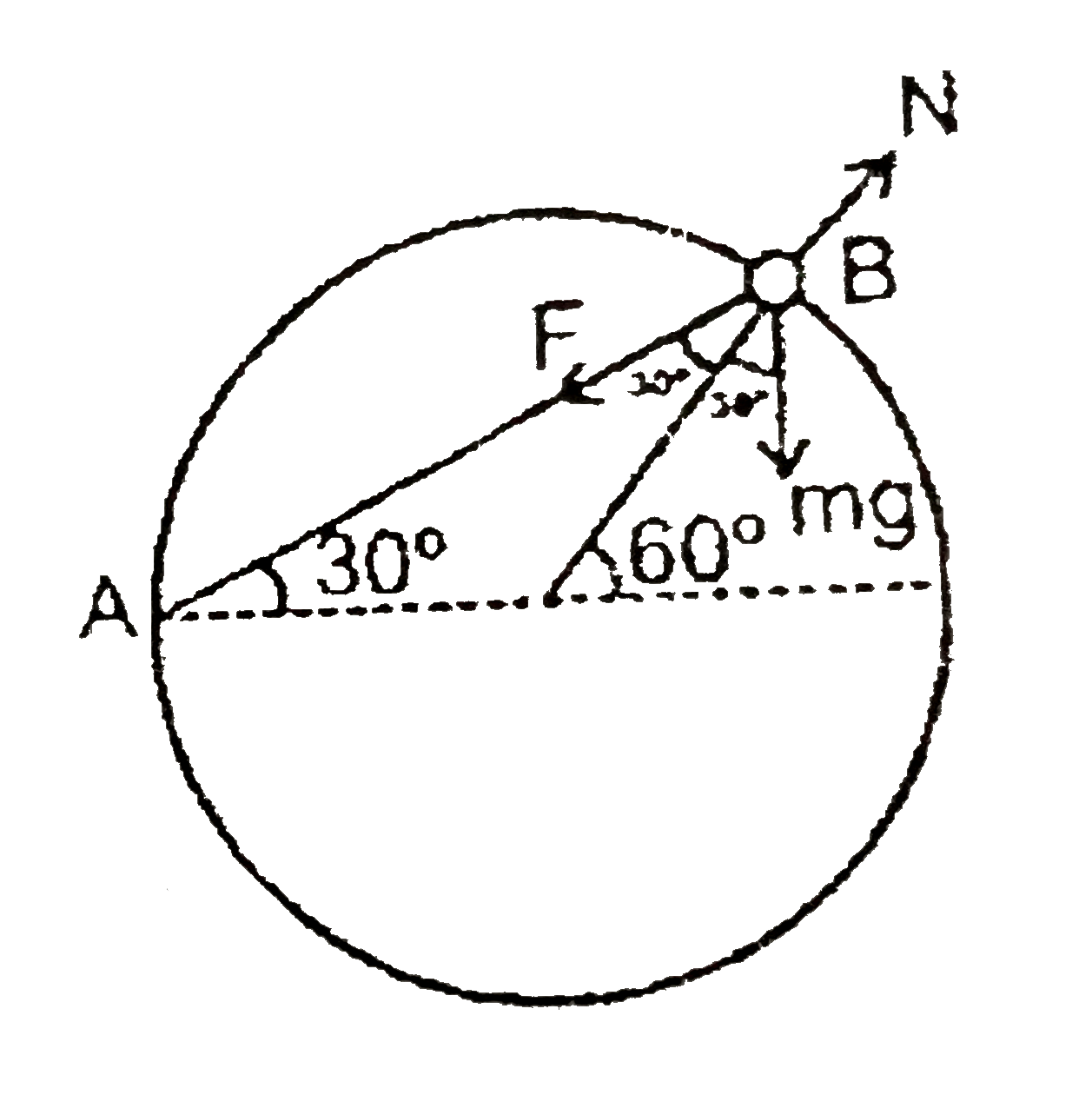
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, the blocks A,B and C of mass m each have accelerations a1,a2 and a3 respectively. F1 and F2 are external forces of magnitude 2mg and mg respectively.
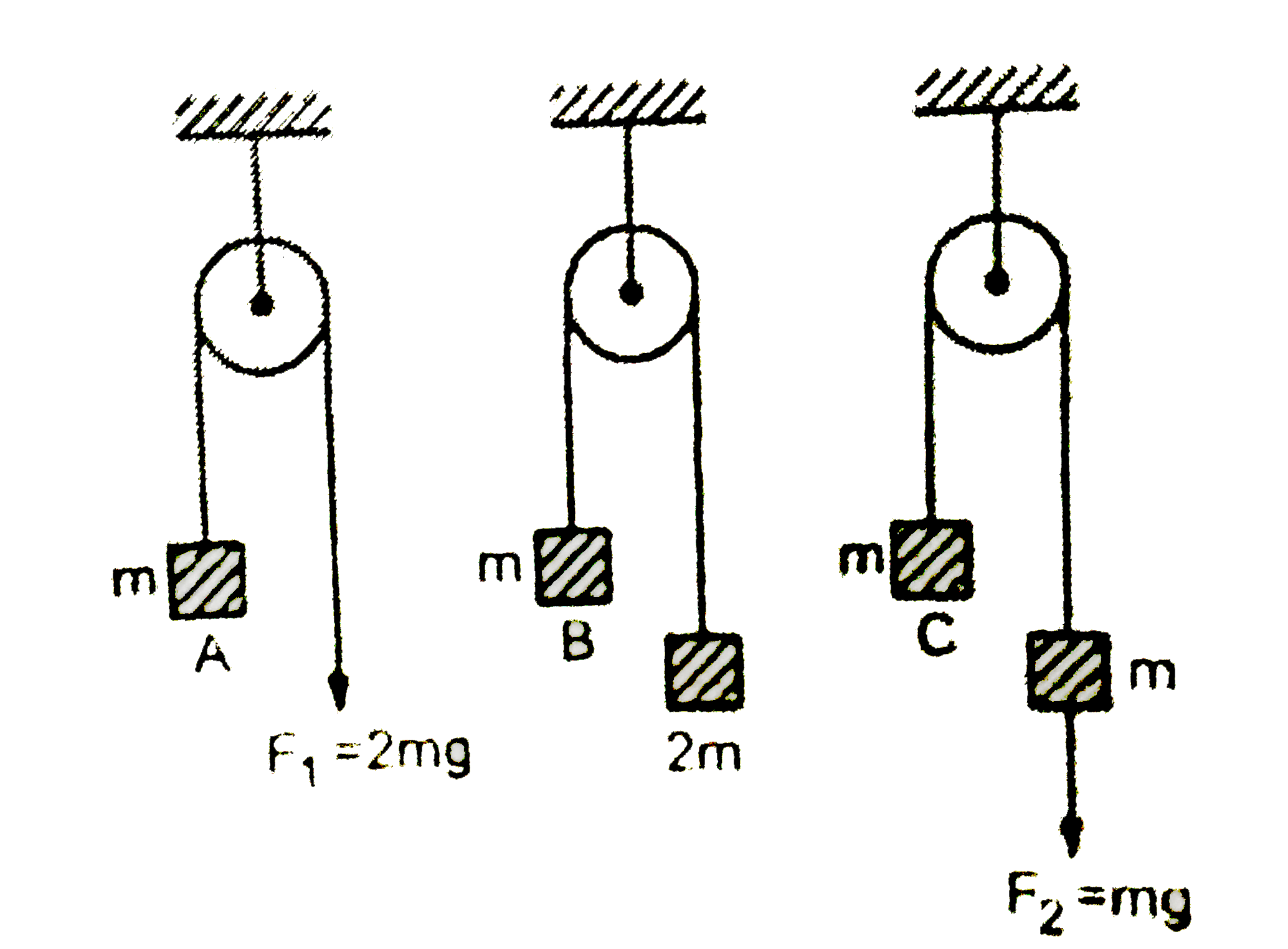 Aa1=a2=a3Ba1>a2>a3Ca1=a2,a2>a3Da1>a2,a2=a3
Aa1=a2=a3Ba1>a2>a3Ca1=a2,a2>a3Da1>a2,a2=a3In fig the blocks A,B,and C of mass m each have acceleration a1,a2,anda3, repectively. F1andF2 are external force of magnitude 2mgandmg, respectively. Then
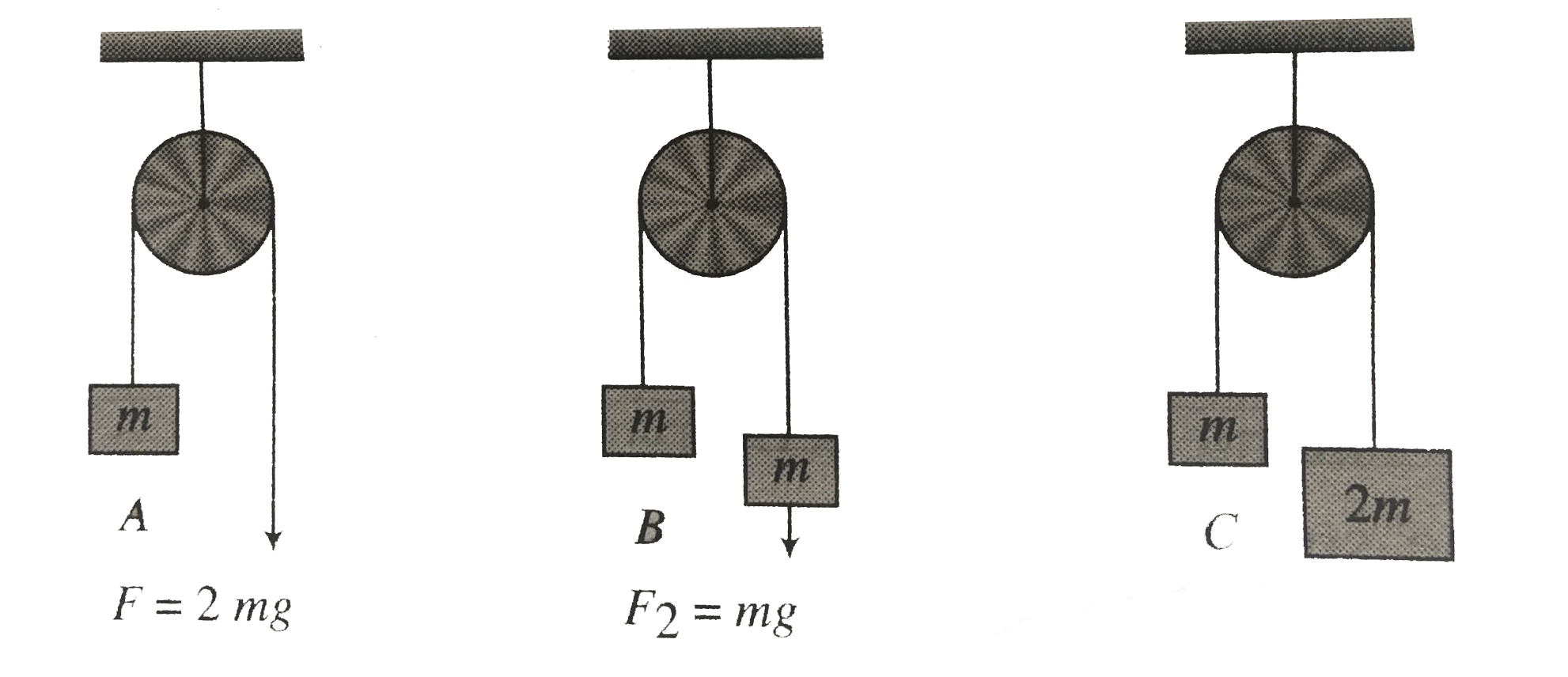 Aa1≠a2≠a3Ba1=a2≠a3Ca1>a2>a3Da1≠a2=a3
Aa1≠a2≠a3Ba1=a2≠a3Ca1>a2>a3Da1≠a2=a3In the figure the block A,B and C of mass m each, have acceleration a1,a2&a3 respectively. F1&F2 are external forces of magnitude 2 mg and mg respectively :
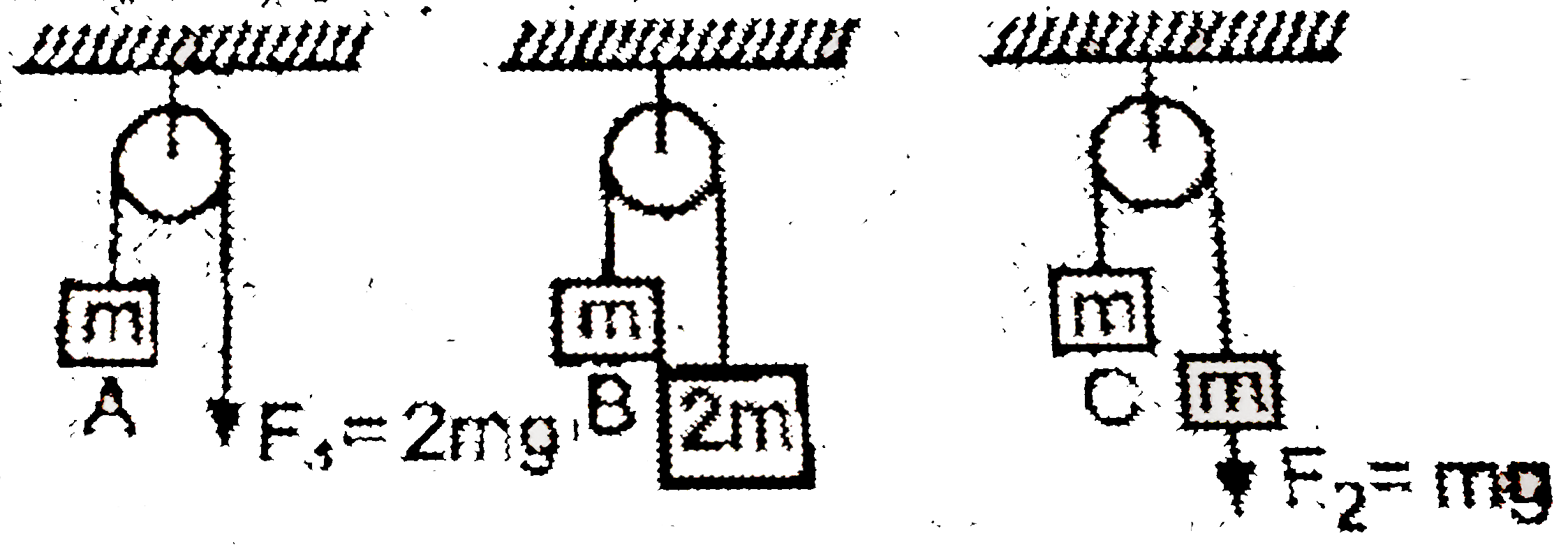 Aa1>a3>a2Ba1=a2,a2=a3Ca1=a2=a3Da1>a2,a2=a3
Aa1>a3>a2Ba1=a2,a2=a3Ca1=a2=a3Da1>a2,a2=a3
In the figure, blocks A, B and C of mass m each have acceleration a1, a2 and a3 respectively. F1 and F2 are external forces of magnitudes 2mg and mg respectively, then :
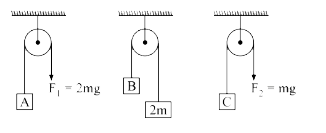
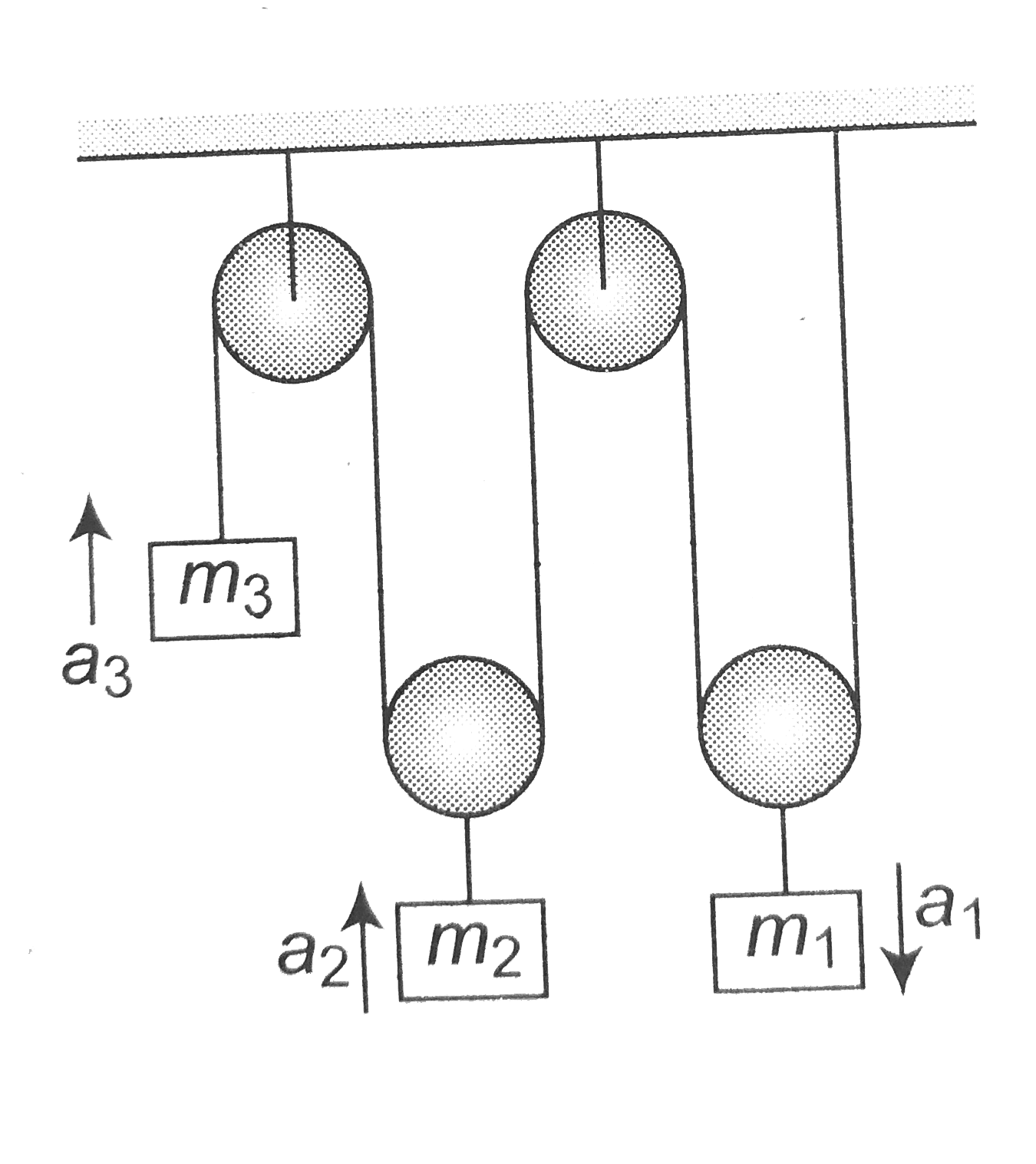
View SolutionIn the adjacent figure, all the pulleys are frictioniess and massless, all the stringes are also massless. The relation between a1,a2 and a3 is (where a1,a2 and a3 are the acceleration of masses m1,m2 and m3 respectively in the direction as shown in the figure)
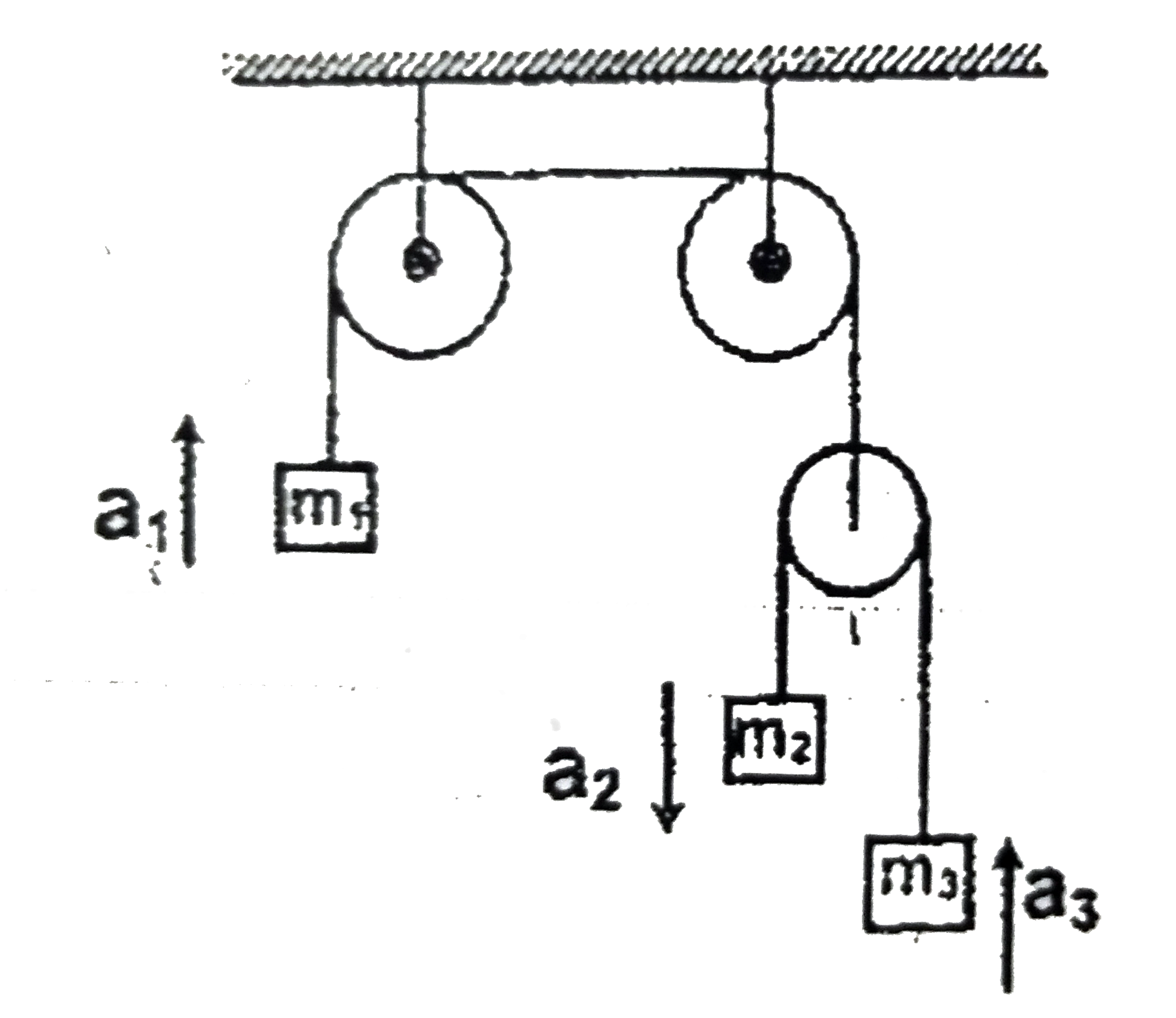
View SolutionIf the blocks are moving as shown in the figure the relation between a1 , a2 and a3 will be.
View SolutionThree rectangles A1,A2 and A3 have the same area Their lengths a1,a2 and a3 respectively are such that a1<a2<a3. Cylinders C1,C2 and C3 are formed from A1,A2 and A3 respectively by joining the parallel sides along the breadth. Then,
View SolutionIf pulleys shown in the diagram are smooth and massless and a1 and a2 are acceleration of blocks of mass 4 kg and 8 kg respectively, then -

View Solution