A car is climbing the hill of slope θ1=53∘ at a constant speed v. If the slope decreases abruptly to θ2=37∘ at point A, determine the acceleration a of the car just after passing point A if the driver does not change the throttle setting or shift into a different gear.

The correct Answer is:6
Distance travelled = 10 m , displacement = 6 m , average velocity = 1.2m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
A car is moving along the circle x2+y2=a2 in the anti-clockwise direction with a constant speed. The x-y plane is a rough horizontal stationary surface. When the car is at the point (acosθ,asinθ), the unit vector in the direction of the friction force acting on the car is
Acosθˆi+sinθˆiBcosθˆi+sinθˆiC−cosθˆi−sinθˆjD−cosθˆi+sinθˆjGenerally, we consider that during slowing of a moving automobile, its retardation is constant, but in practice this is seldom the case. Under many circumstances, especially at high speed, we usually apply the brakes slowly at first and then more strongly as the car slows. The braking force therefore depends on the time during the interval over which the car is slowing and acceleration changes with time.
ax(t)=vA−vxdt=Fx(t)m
∫vxv0xdVx=∫10Fx(t)mdt
∴Vx=V0x+1m∫10Fx(t)dt
x(t)=x0+∫10Vx(t)dt
An example for the same is discussed here.
A car of mass m = 1000 kg is moving with 25 m/s. The driver begins to apply the brakes so that the magnitude of the braking force increases linearly with time at a rate of 2000 N/s.
Read the above passage carefully and answer the following questions.
How much time passes before the car comes to rest?A5 secB4 secC8 secD6.5 secGenerally, we consider that during slowing of a moving automobile, its retardation is constant, but in practice this is seldom the case. Under many circumstances, especially at high speed, we usually apply the brakes slowly at first and then more strongly as the car slows. The braking force therefore depends on the time during the interval over which the car is slowing and acceleration changes with time.
ax(t)=vA−vxdt=Fx(t)m
∫vxv0xdVx=∫10Fx(t)mdt
∴Vx=V0x+1m∫10Fx(t)dt
x(t)=x0+∫10Vx(t)dt
An example for the same is discussed here.
A car of mass m = 1000 kg is moving with 25 m/s. The driver begins to apply the brakes so that the magnitude of the braking force increases linearly with time at a rate of 2000 N/s.
Read the above passage carefully and answer the following questions.
Find the velocity of the car at t = 10 sec.AzeroB10 m/sC15 m/sDNone of the above
A boy throws a stone with a speed of V0=10 m/sec at an angle of θ0=30∘ to the horizontal Find the position of the stone wrt the point of projection just after a time t = 1/2 sec.
View SolutionA truck is travelling due north descending a hill of slope angle θ=tan–1(0.1) at a constant speed of 90km/hr. At the base of the hill there is a gentle curve and beyond that the road is level and heads 30∘ east of north. A south bound police car is travelling at 80km/hr along the level road at the base of the hill approaching the truck. Find the velocity of the truck relative to police car in terms of unit vectors ˆi,ˆj and ˆk . Take x axis towards east, y axis towards north and z axis vertically upwards.
View SolutionThere are two hills A and B and a car is travelling towards hill A along the line joining the two hills. Car is travelling at a constant speed u. There is a wind blowing at speed u in the direction of motion of the car (i.e., from hill B to A). When the car is at a distance x1 from A and x2 from B it sounds horn (for very short interval). Driver hears the echo of horn from both the hills at the same time.
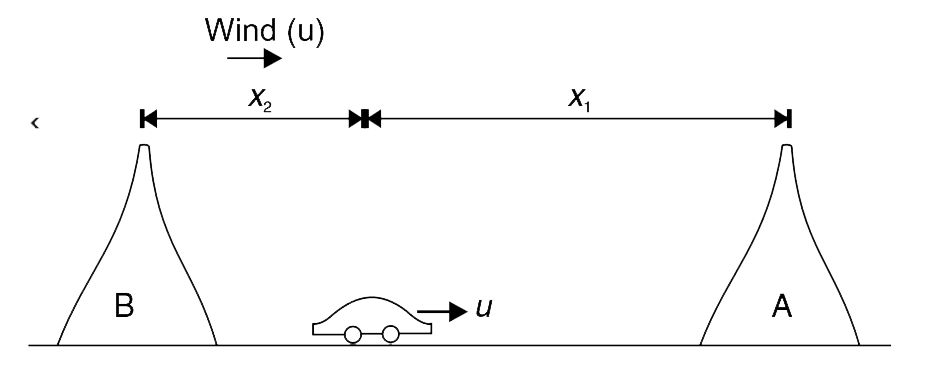
Find the ratio x1x2 taking speed of sound in still air to ve V.
View SolutionTwo point masses of mass m and equal and opposite charge of magnitude q are attached on the corners of a non-conducting uniform rod of mass m and the system is released from rest in uniform electric field E as shown in figure from θ=53∘

(i) Find angular acceleration of the rod just after releasing
(ii) What will be angular velocity of the rod when it passes through stable equilibrium.
(iii) Find work required to rotate the system by 180∘.
View SolutionA pendulum bob can swing along a ciircular path on a smooth inclined plane, as shown in Fig. 3E.31, where m=1.2kg,1=.075m,θ=37∘. At the lowest point of the circle the tension in the sting is T=110N. Determine
(a) the speed of the bob at the lowest point,
(b) the speed of the bob at the highest point on the circle and
(c) the tension in the string at the highest position
(a)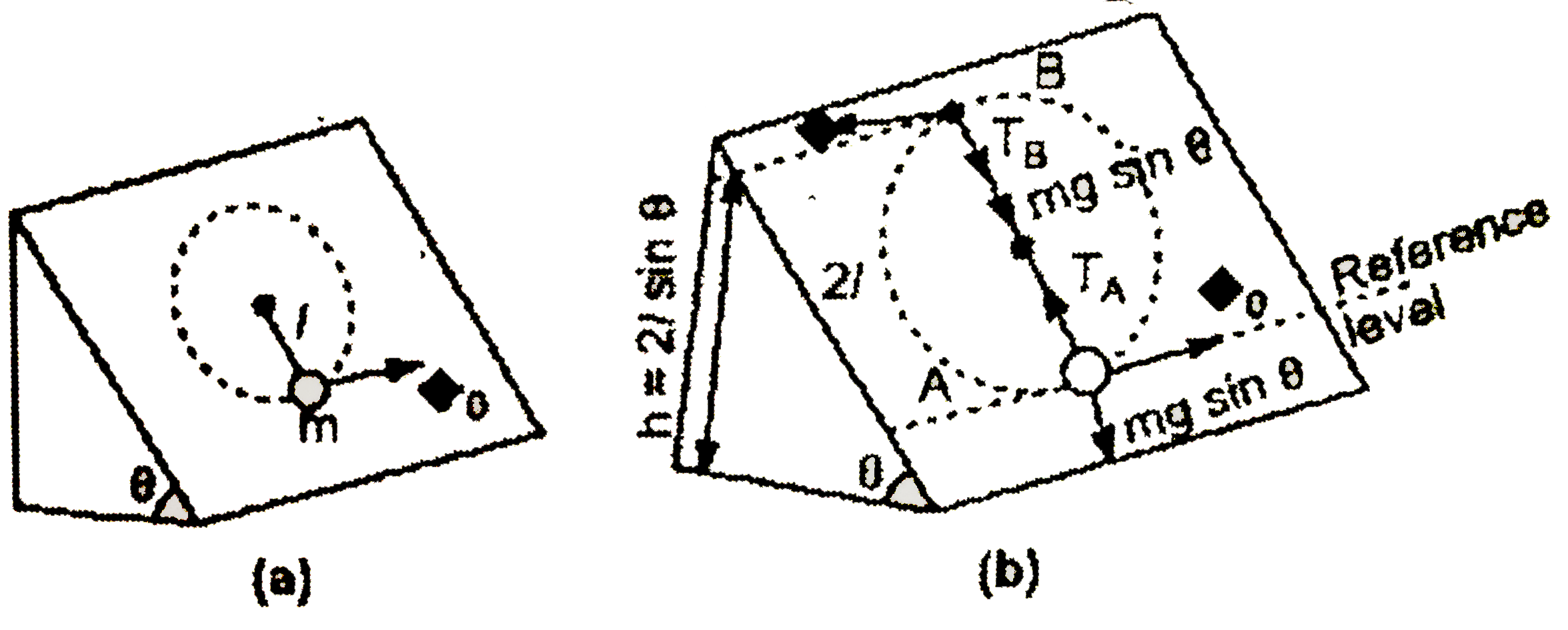
View Solution

