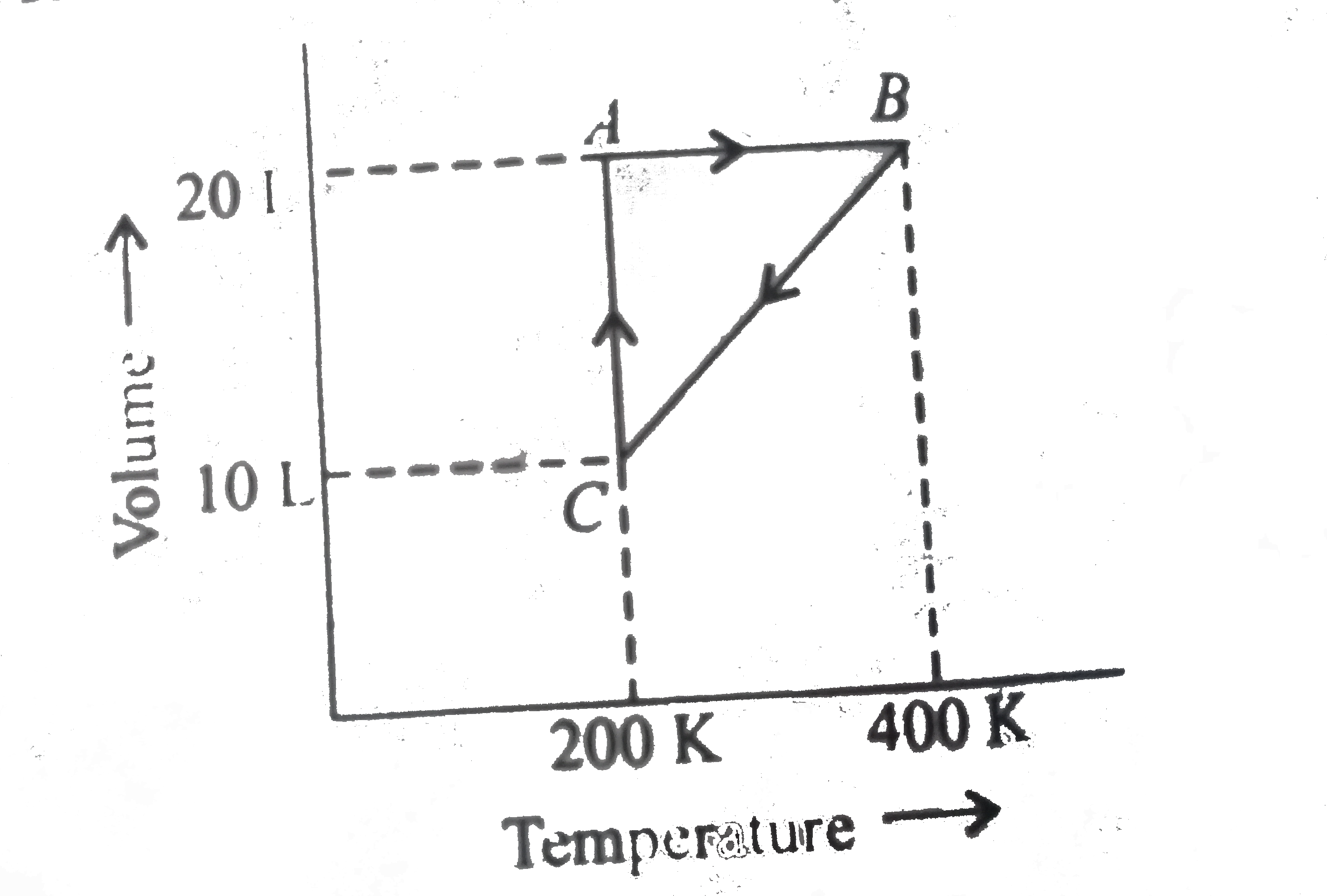
Isothermal expansion from , isochoric pressure increase from , isobaric compression from , isochoric pressure drop from .
Topper's Solved these Questions
- THERMODYNAMICSBook:RESONANCEChapter:THERMODYNAMICSExercise:B-3
Explore 1 Video
- THERMODYNAMICSBook:RESONANCEChapter:THERMODYNAMICSExercise:C-1
Explore 1 Video
- THERMODYNAMICSBook:RESONANCEChapter:THERMODYNAMICSExercise:B-1
Explore 1 Video
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:CHEMISTRY
Explore 50 Videos
Similar Questions
Knowledge Check
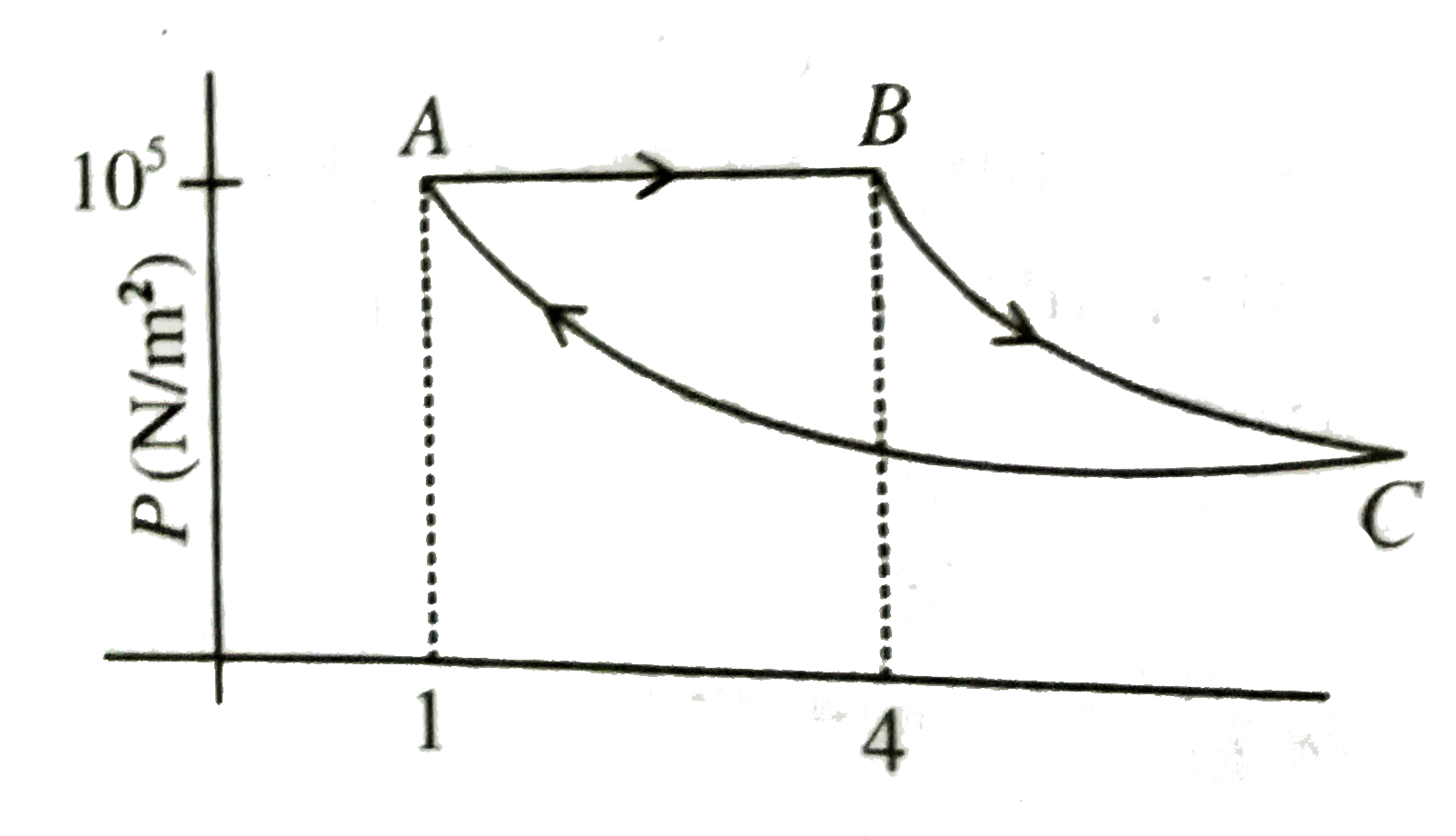
The process which occurs in going from B→C isAIsothermalBAdiabaticCIsobaricDIsochoricA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
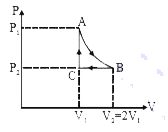
Find pressure at C.A10564N/m2B10532N/m2C10512N/m2D1056N/m2n mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
A→B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2=2V1 and pressure changes from P1 to P2
B→C : Isobaric compression at pressure P2 to initial volume V1
C→A : Isochoric change leading to change of pressure from P2 toP1 .
Total work done in the complete cycle ABCA is :
 A0BnRT(ln2+12)CnRTln2DnRT(ln2−12)
A0BnRT(ln2+12)CnRTln2DnRT(ln2−12)
100 mol of an ideal monatomic gas undergoes the following thermodynamic process as shown in the figure ( P−V or Pressure-Volume plots are shown) A→B: Isothermal expansion B→C Adiabatic expansion
C→D: Isobaric compression
D→A: Isochoric process
The heat transfer along the process AB is 9×104J. The net work done by the gas during the cycle is k×104J. Find k, (Take R=8(~J).(K)−1(~mol)−1 )
'(##CEN_KSR_PHY_JEE_C15_E01_030_Q18##)'
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View SolutionFor the reaction : A+2B→C+D, the expression of rate of reaction will be :
View SolutionFor the reaction, A+2B→C, the differential from of the rate law is:
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
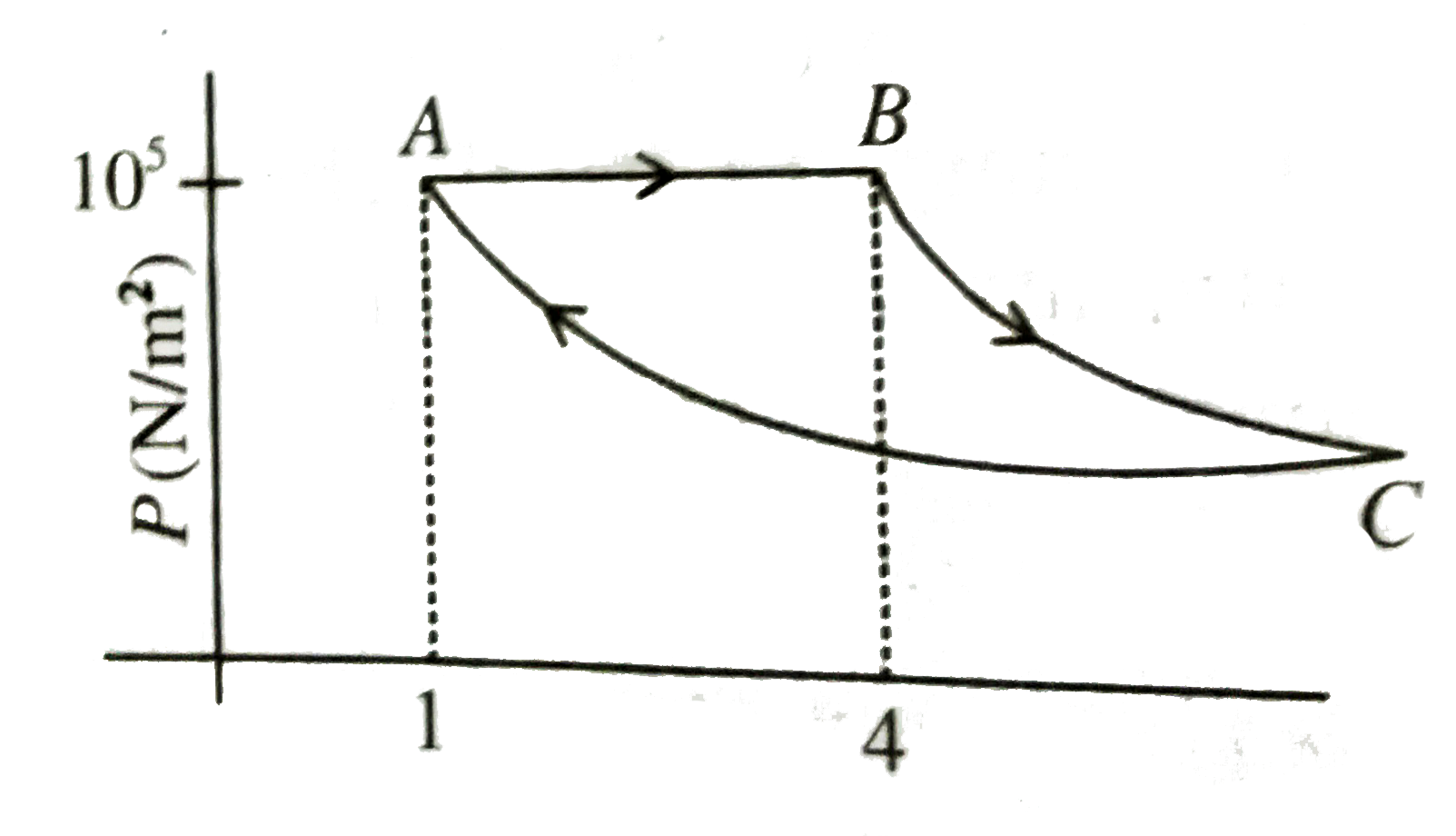 Find volume at C.
Find volume at C.
View Solution
