Prove that En=−13.6×z2n2eV/a→m for nth orbit in single electron species.
The correct Answer is:The total energy of an electron revolving in a particular orbit is
T.E.=K.E.+P.E.
where P.E.=Potential energy, K.E. =Kinetic energy, T.E.=Total energy
The K.E. of an electron=12mv2
and the P.E. of an electron =−KZe2r
Hence, T.E.=12mv2−KZe2r
we know that, mv2r=KZe2r2 or mv2=KZe2r
Substituting the value of mv2 in the above equation:
T.E.=KZe22r−KZe2r=−KZe22r
So, T.E.=−KZe22r
substituting the value of 'r' in the equation of T.E.
Then T.E.=−KZe22×4π2Ze2mn2h2=−2π2Z2e4mK2n2h2
Thus, the total energy of an electrons in nth orbit is given by
T.E.=En=−2π2me4k2h2(z2n2)...(iv)
Putting the value of m,e,h and π we get the expression of total energy
En=−13.6Z2n2eV/a→mn↑⏐
⏐
⏐⏐T.E.↑⏐
⏐
⏐⏐;Z↑⏐
⏐
⏐⏐T.E.⏐⏐
⏐
⏐↓
Step by step video, text & image solution for Prove that E_(n)=-13.6xxz^(2)/n^(2) eV//atom for n^(th) orbit in single electron species. by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NUCLEAR CHEMISTRYBook:RESONANCEChapter:NUCLEAR CHEMISTRYExercise:Exercise-1
Explore 47 Videos
- NUCLEAR CHEMISTRYBook:RESONANCEChapter:NUCLEAR CHEMISTRYExercise:PART -II
Explore 32 Videos
- NUCLEAR CHEMISTRYBook:RESONANCEChapter:NUCLEAR CHEMISTRYExercise:MISCELLANEOUS SOLVED PROBLEMS (MSPs)
Explore 9 Videos
- NITROGEN CONTAINING COMPOUNDSBook:RESONANCEChapter:NITROGEN CONTAINING COMPOUNDSExercise:ORGANIC CHEMISTRY(Nitrogen containing Compounds)
Explore 30 Videos
- P BLOCK ELEMENTSBook:RESONANCEChapter:P BLOCK ELEMENTSExercise:PART -II
Explore 24 Videos
Similar Questions
Electron present in single electron specie jump from energy level 3 to 1 .Emitted photons when passed
through a containig excited He^(+) ino cause further excition to same higher energy level (Given
En=−13.6(Z2n2).Determine
(i) Atomic number of single electron specie.
(ii) principle quantum number of inital excited level & higher energy level of He+.
View Solutionrn,z= Radius of nth orbit of a single electron species having atomic number 'z'
un,z= Velocity of electron in nth orbit of a single electron specie having atomic number 'z'
En,z= Magnitude of total energy of electron in nth orbit of a single electron species having atomic number 'z'.
Kn,z= Magnitude of kinetic energy of electron in nth orbit of a single electron species having atomic number 'z'
Pn,z= Magnitude of potential energy of electron in nth orbit of a single electron species having atomic number 'z'
fn,z= Frequency of electron in nth orbit of a single electron species having atomic number 'z'.
Tn,z= Time period of electron in nth orbit of a single electron species having atomic number 'z'
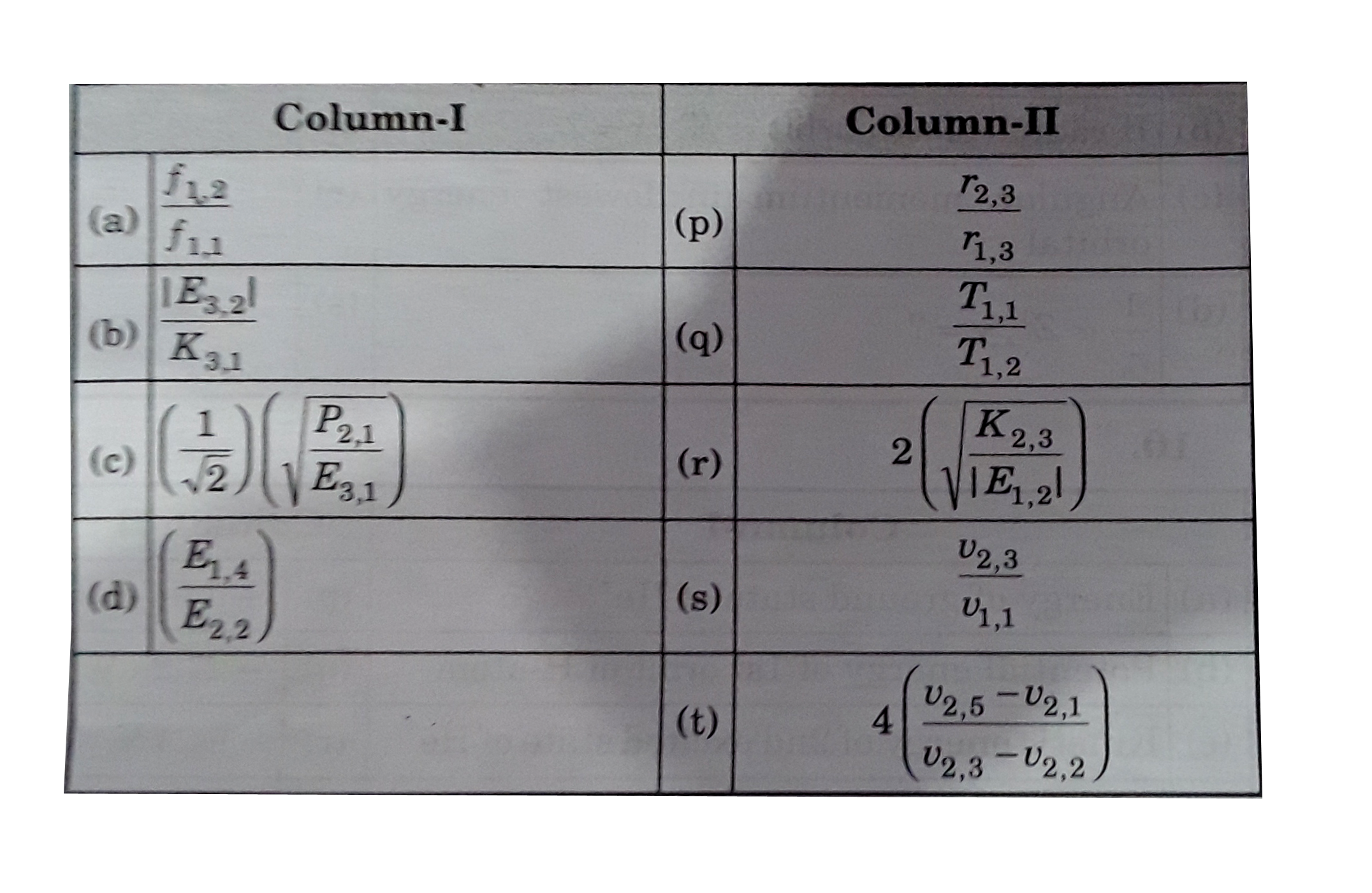
View Solution
Knowledge Check
The energy of electron in the nth orbit of hydrogen atom is expressed as En=−13.6n2eV. The shortest and longest wavelength of Lyman series will be
A910Å,1213ÅB5463Å,7858ÅC1315Å,1530ÅDNone of theseIn the nth orbit, the energy of an electron En=−13.6n2eV for hydrogen atom. The energy required to take the electron from first orbit to second orbit will be
A10.2eVB12.1eVC13.6eVD3.4eVEnergy of the electron in nth orbit of hydrogen atom is given by En=−13.6n2eV. The amount of energy needed to transfer electron from first orbit to third orbit is
A13.6eVB3.4eVC12.09eVD1.51 eV
The energy of electron in hydrogen atom is En=−13.6n2eV, Where n=1, 2,3,......Show that (i) the electron in hydrogen atom cannot have an energy of -6.8eV. (ii) spacing between the lines (consecutive energy levels) within the given set of observed hydrogen spectrum decreases as n increases.
View SolutionThe energy of an electron moving in nth Bohr's orbit of an element is given by En=−13.6n2Z2 eV/ atom (Z=atomic number). The graph of E vs. Z2 (keeping "n" constant) will be :
View SolutionThe energy of an electron in the nth orbit is given by En=−13.6/n2eV. Calculate the energy required to excite an electron from ground state to the second excited state.
View SolutionHow many unique spectral lines are emitted when e− returns from nth2 orbit to nth1 orbit in a sample of H-like species ?
View SolutionThe radius of nth orbit of a single electron species is 0.132n2A∘. Identify the element.
View Solution

