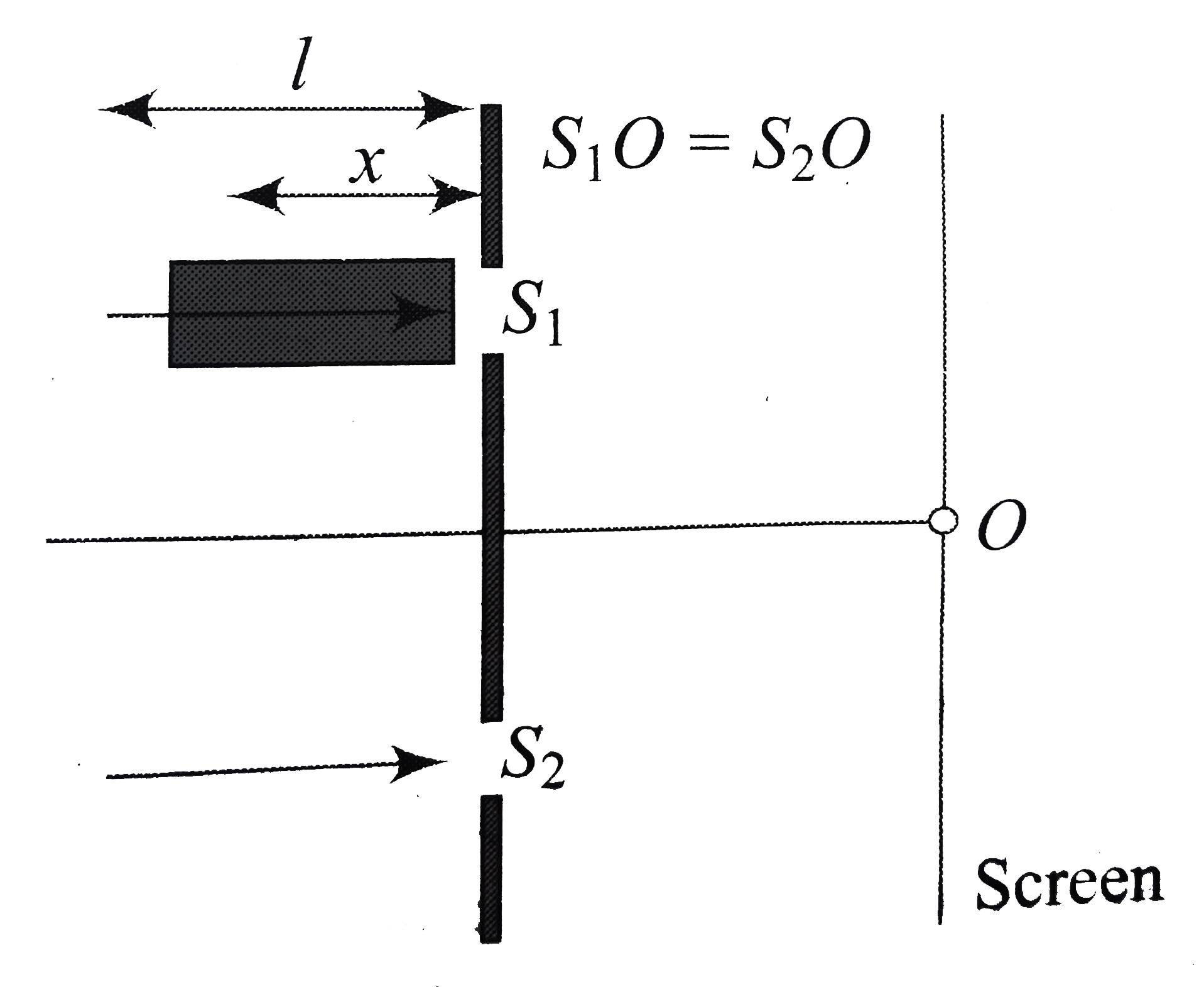
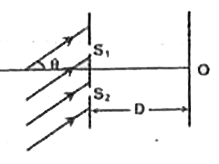
In figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit S1 passes through a medium of variable refractive index μ=1+ax (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on S1. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength λ in air) is
λl
λl2
l2λ
None of these
The correct Answer is:B
When light passes through a medium of refractive index μ, the optical path it travels is (μt).
Therefore, berore reaching O light through S1 travels (μl+b) distance while that through S2 travels a distance (l+b)
i.e.: path difference =(μl+b)−(l+b)=(μ−1)l.
For a smalll element 'dx' path difference Δx=[1(+ax)−1]dx=axdx
For the whole length ,
Δx=∫loaxdx=al22
For a minima to be at 'O'.
Δx=(2n+1)λ2
i.e.:al22=(2n+1)λ2.
For minimum 'a',n=0⇒al22=λ2⇒a=λl2
Topper's Solved these Questions
- WAVE OPTICSBook:RESONANCEChapter:WAVE OPTICSExercise:Exercise-2 (Part-2)
Explore 5 Videos
- WAVE OPTICSBook:RESONANCEChapter:WAVE OPTICSExercise:Exercise-2 (Part-3)
Explore 5 Videos
- WAVE OPTICSBook:RESONANCEChapter:WAVE OPTICSExercise:Exercise-1 (Part-2)
Explore 13 Videos
- WAVE ON STRING Book:RESONANCEChapter:WAVE ON STRING Exercise:Exercise- 3 PART I
Explore 19 Videos
Similar Questions
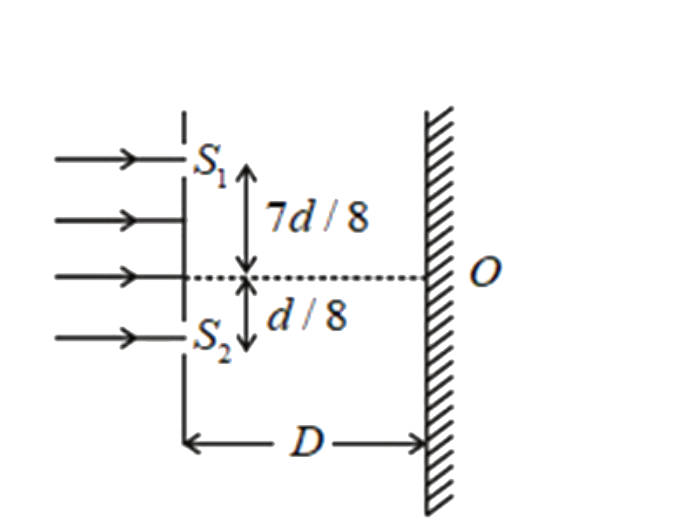
In the figure , if a parallel beam of white light is incident on the plane of the slits S1andS2 then the distance of the nearest white spot on the screen from O is [ Assume D>>d,d>>λ ]
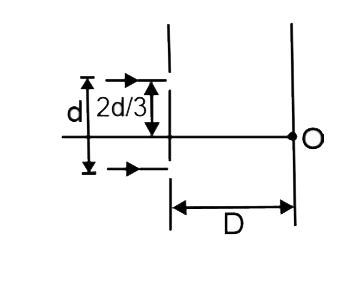
View SolutionIn the figure shown if a parallel beam of white light is incident on the plane of the slits then the distance of the white spot on the screen from O is [Assume <<D,λ<<d]
View Solution
Knowledge Check
In YDSE,D=1m,d=4mm and λ=12mm in the figure shown, a parallel beam of light is incident on the plane of the slits of YDSE. Light incident on the slit s1, passes through a medium of variable refractive index μ=(2x+1) (where x is the distance from the plane of slits in mm) up to a distance l=1mm before falling on s1. Rest of the space filled with air. Then choose the correct option (s):
 APosition of central brigh fringe is at a distanc y=1√3m above the central lineBPosition of central bright fringe is at a distance y=12m above the central lineCNumber of maxima obtaining on the screening is 7DNumber of maxima obtaining on the screening is 8
APosition of central brigh fringe is at a distanc y=1√3m above the central lineBPosition of central bright fringe is at a distance y=12m above the central lineCNumber of maxima obtaining on the screening is 7DNumber of maxima obtaining on the screening is 8Two different color beams (yellow and blue) from a point source are incident on both slits of a Young's double-slit experiment setup
AThere will be no interference pattern seen on the screenBThere will be interference pattern and where there is constructive interference the spot will be greenCThere will be alternate bands of yellow, blue, and dark regions with equal separation between themDThere will be yellow and blue light interference patterns which are slightly separated from each otherbecause the angles at which the maxima and minima occur for the two wavelengths are differentIf one of the two slits og Young's double-slit experiment is painted so that it transmits half the light intensity as the second slit, then
Athe fringe system will altogether disappearBthe bright fringes will become brighter and the dark fringes will become darkerCboth dark and bright fringe will become darkerDdark fringe will become brighter and bright fringe darker
How will the interference pattern in Youngs double slit experiment change, when distance between the slits S1andS2 are reduced
View SolutionA parallel beam of light (λ=5000Å) is incident at an angle θ=30∘ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I_0. Point O is equidistant from S1andS2. The distance between slits is 1mm.
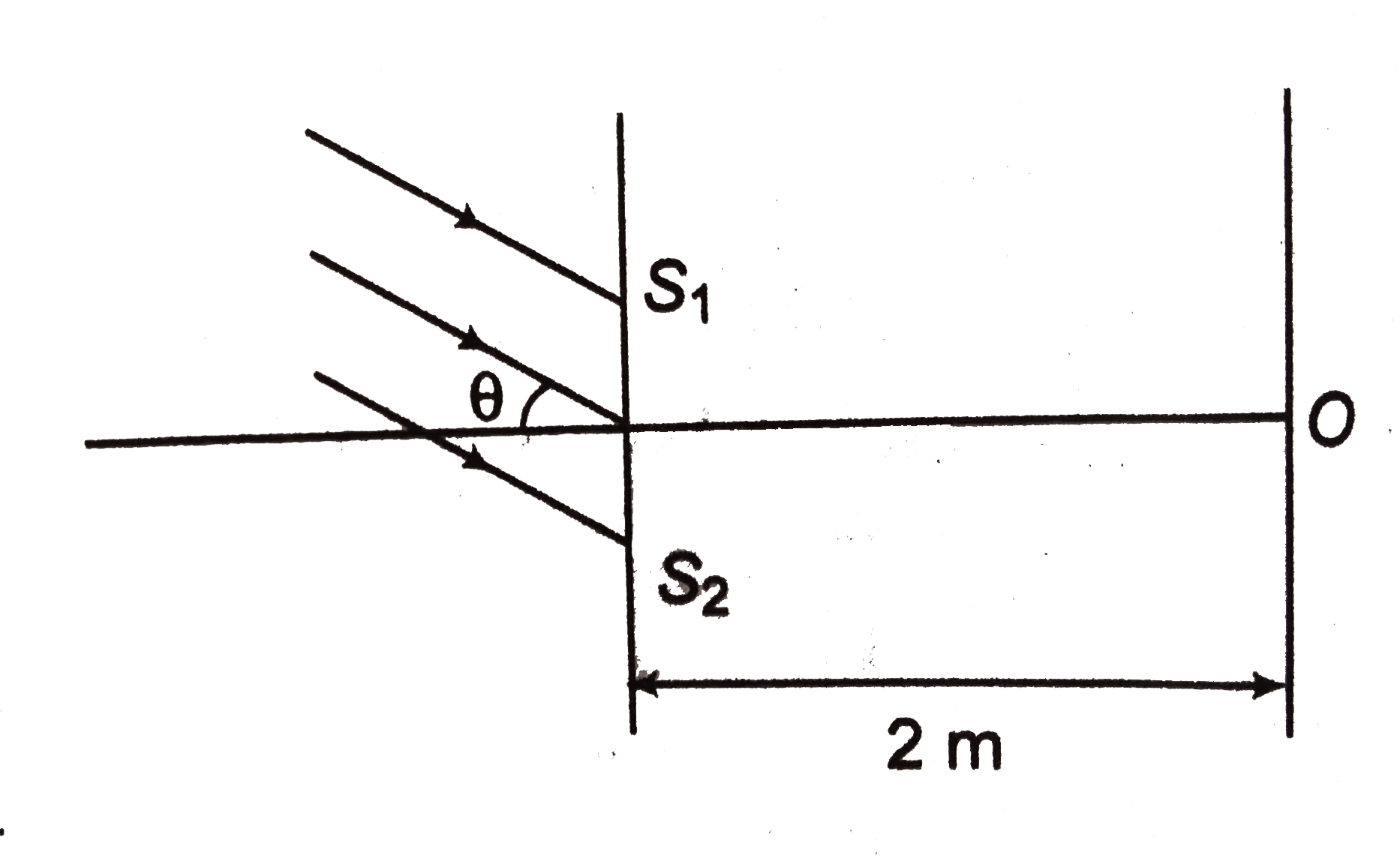
View SolutionIn Young’s double slit experiment, the distance between the two slits is made half, then the fringe width will become
View SolutionIn Young's double slit experiment parallel monochromatic light is incident on both the slits at an angle as shown in the figure. To obtain the central maxima at on the screen we can
View SolutionIn a Young's double slit experiment, the separation of the two slits is doubled. To keep the samme spacing of fringes, the distance D of the screen from the slits should be made
View Solution

