Draw phase diagram for a series LCR circuit with alternating voltage source, determine the expression for the impedance of the circuit.
OR
Draw a diagram of AC generator and describe it.Derive an expression for instantaneous value of induced emf.
RLC SERIES CIRCUIT WITH AN AC SOURCE:
From the phasor diagram
V=√(IR)2+(IXL−IXC)2=I√(IR)2+(IXL−IXC)2=IZ,Z=√(R)2+(XL−XC)
tanϕ=I(XL−XC)IR=(XL−XCR
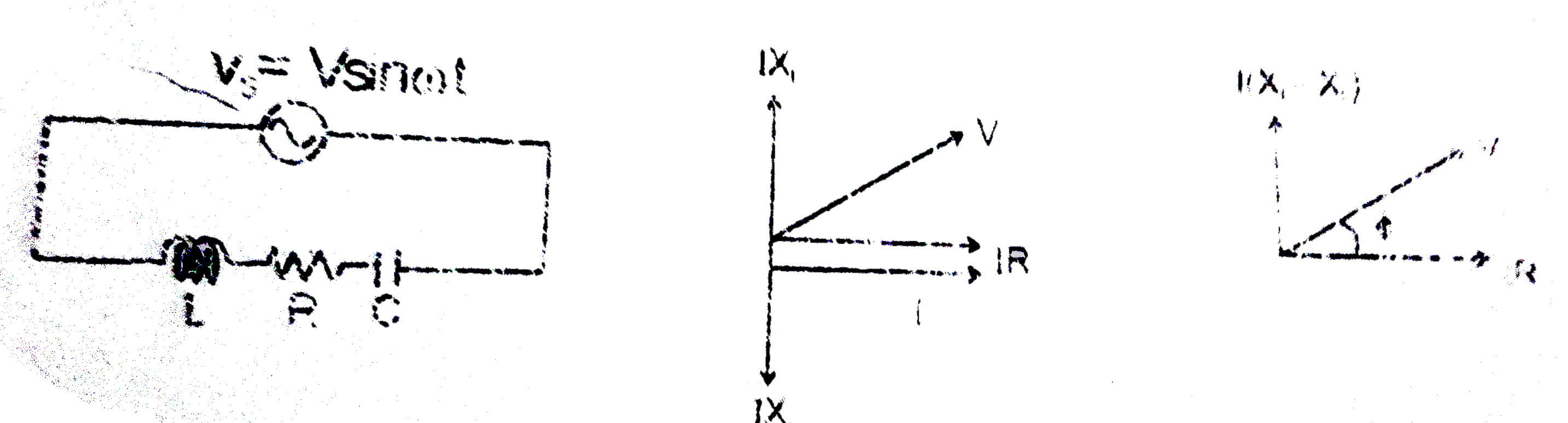
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - A.L.P
10 Videos
- ALTERNATING CURRENTBOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - SOLVED MISCELLANEOUS
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -3 Part-2
3 Videos
- ATOMIC PHYSICSBOOK - RESONANCECHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
Knowledge Check
In series LCR AC circuit, the voltage of the source at any instant is equal to
AThe sum of the maximum voltage across the elementsBThe voltage drop across the resistorCThe sum of the instantaneous voltages across the elementsDThe sum of the rms voltages across the elementsWhen the frequency of the AC voltage applied to a series LCR circuit is gradually increased from a low value, the impedance of the circuit
Amonotonically increasesBfirst increases and then decreasesCfirst decreases and then increasesDmonotonically decreases
Derive an expression for the impedance of an a.c. circuit consisting of an inductor and a resistor.
View SolutionDerive an expression for the impedance of an a.c. circuit consisting of an inductor and a resistor.
View SolutionDraw a labelled diagram of compound microscope. Derive expression for its magnifying power.
View SolutionDraw the phasor diagram of a series LCR connected across an ac source V=V0sinωt. Hence derive the expression for the impedance of the circuit . Obtain the conditions for the phase angle under which the current is (i) maximum and (ii) minimum.
View SolutionWith the help of a phasor diagram find an expression for impedance (Z) in a series L-C-R circuit.
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View Solution
