A battery of 10 cells each of e.m.f. E=1.5V and internal resistance 0.5Ω has 1 cell wrongly connected. It is being charged by 220V power supply with an external resistance of 47Ω in series. The potential difference across the battery.
The correct Answer is:32V
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the total EMF of the battery
Given that there are 10 cells, each with an EMF of E=1.5V, and one cell is wrongly connected, the effective number of cells contributing to the EMF is 10−1=9.
Total EMF=9×1.5V=13.5V
Step 2: Calculate the internal resistance of the battery
Each cell has an internal resistance of r=0.5Ω. Since one cell is wrongly connected, the total internal resistance contributed by the remaining 9 cells is:
Total Internal Resistance=9×0.5Ω=4.5Ω
Step 3: Calculate the total resistance in the circuit
The total resistance in the circuit includes the external resistance and the internal resistance of the battery:
Total Resistance=Rexternal+Rinternal=47Ω+4.5Ω=51.5Ω
Step 4: Calculate the total voltage supplied by the power supply
The power supply voltage is given as Vpower supply=220V.
Step 5: Calculate the current flowing through the circuit
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=Vpower supply−Total EMFTotal Resistance=220V−13.5V51.5Ω
Calculating the numerator:
220−13.5=206.5V
Now substituting this value into the current formula:
I=206.5V51.5Ω≈4.01A
Step 6: Calculate the potential difference across the battery
The potential difference V across the battery can be calculated using the formula:
V=Total EMF+I×Rinternal
Substituting the values we have:
V=13.5V+(4.01A×4.5Ω)
Calculating the second term:
4.01×4.5≈18.045V
Now substituting this back into the equation for V:
V≈13.5V+18.045V≈31.545V
Final Answer
The potential difference across the battery is approximately 31.55V.
---
Given that there are 10 cells, each with an EMF of E=1.5V, and one cell is wrongly connected, the effective number of cells contributing to the EMF is 10−1=9.
Each cell has an internal resistance of r=0.5Ω. Since one cell is wrongly connected, the total internal resistance contributed by the remaining 9 cells is:
The total resistance in the circuit includes the external resistance and the internal resistance of the battery:
The power supply voltage is given as Vpower supply=220V.
Using Ohm's law, the current I flowing through the circuit can be calculated as:
The potential difference V across the battery can be calculated using the formula:
The potential difference across the battery is approximately 31.55V.
Topper's Solved these Questions
Similar Questions
(a) Find the potential difference between A and B
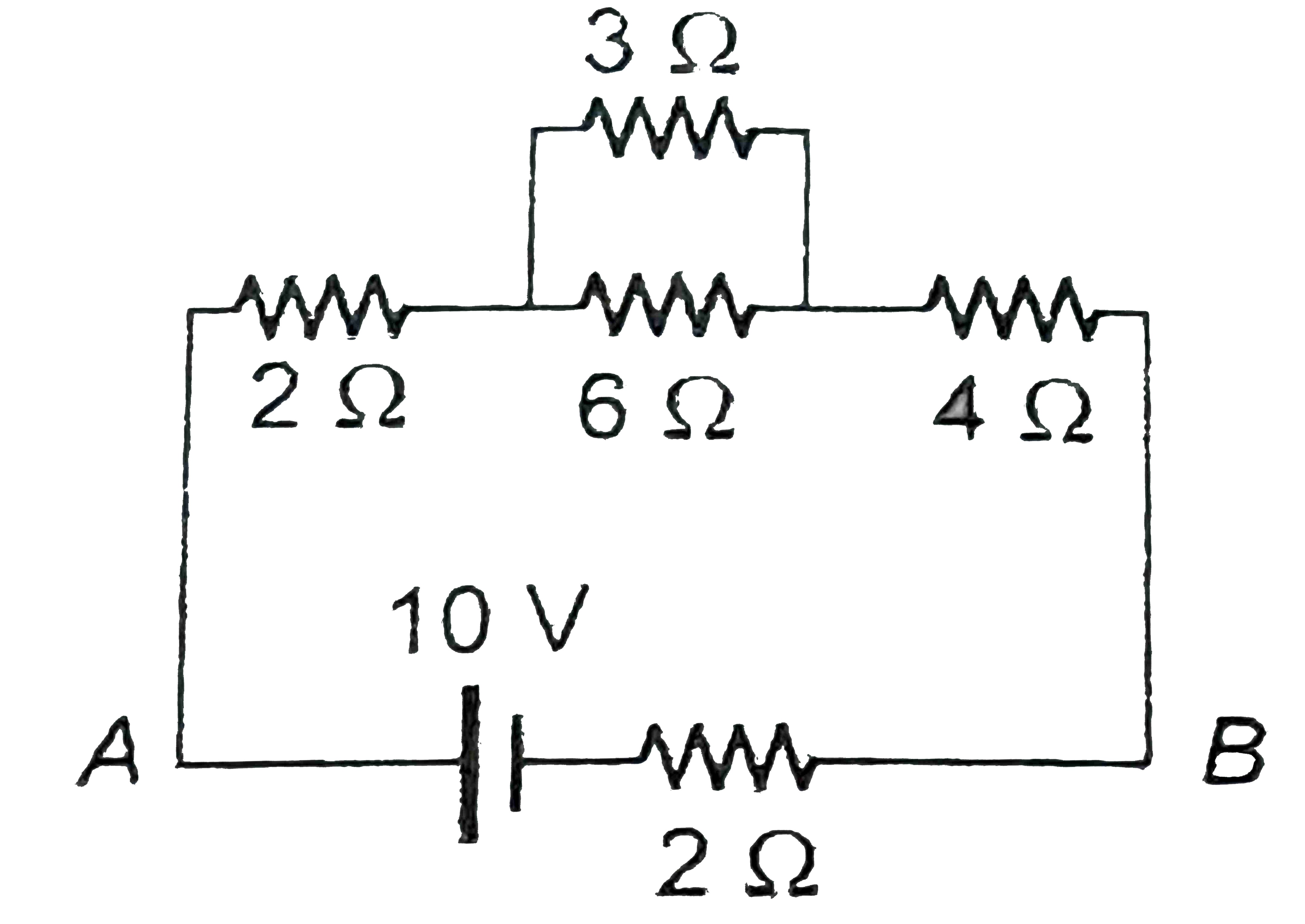
(b) Calculate the current flowing in the circuit and the potential difference across terminals of each cell.
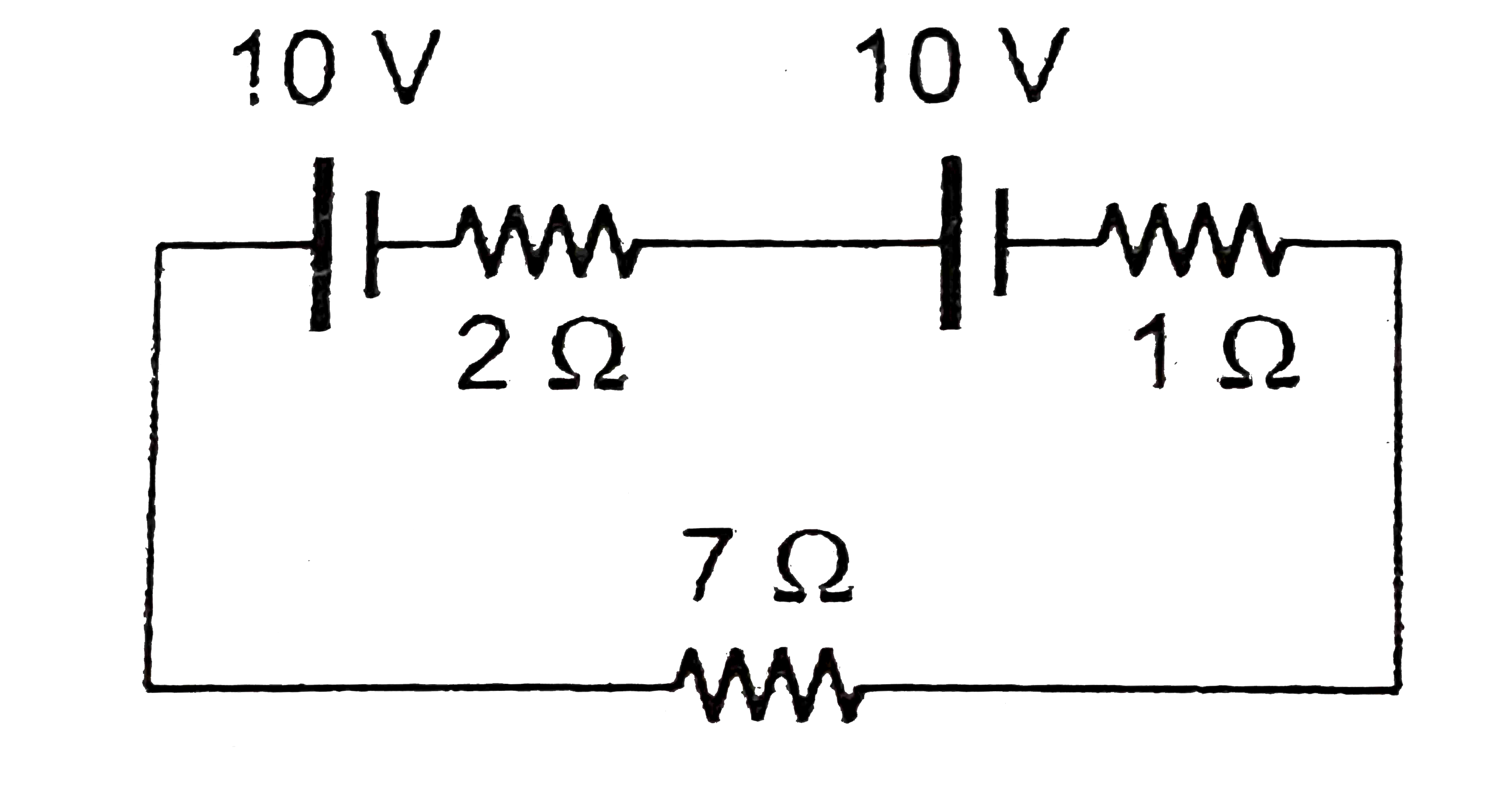
( c) Calculate the potential difference across terminals of each cell.
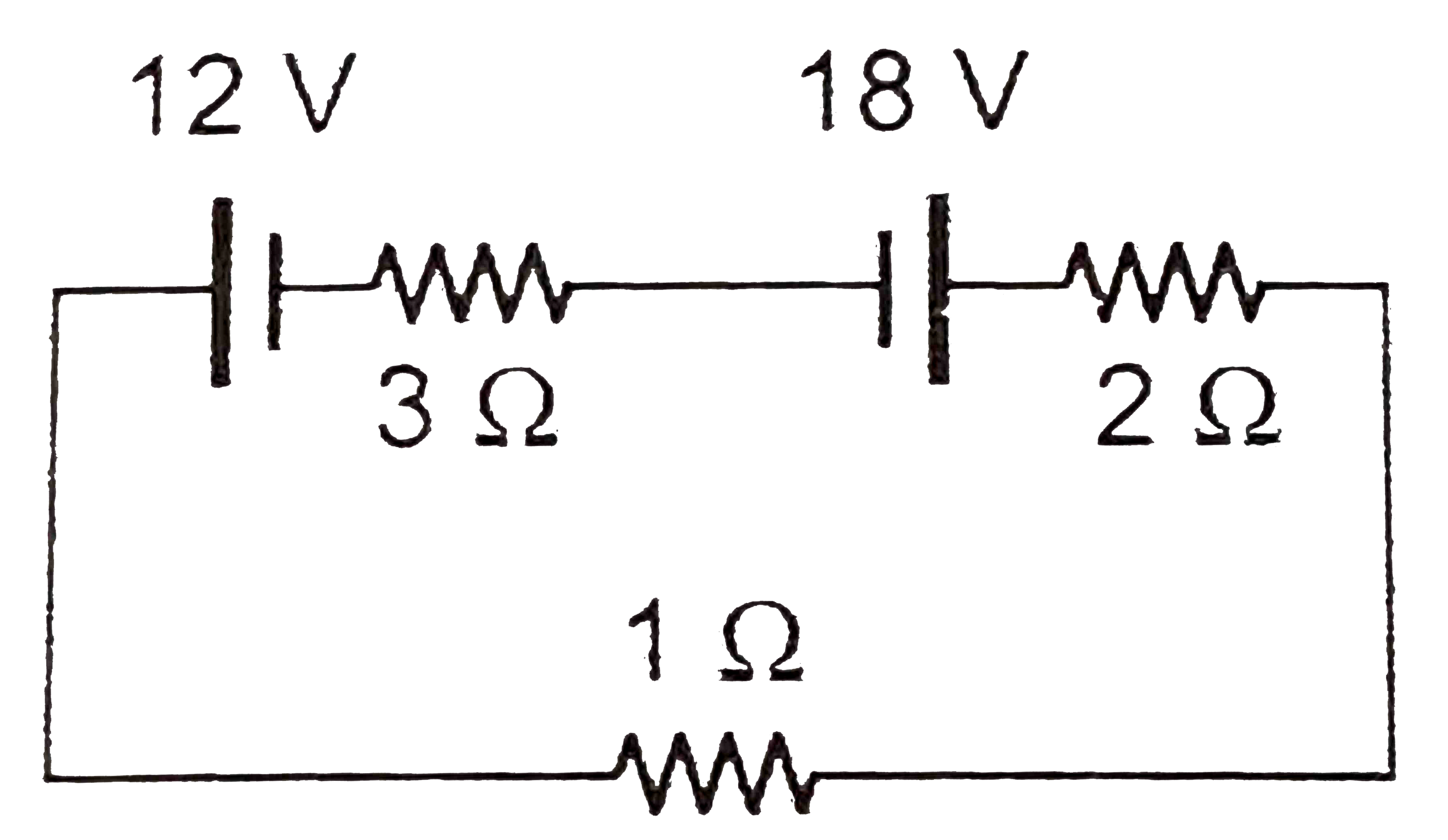
(d) Calculate the potential difference between A and B
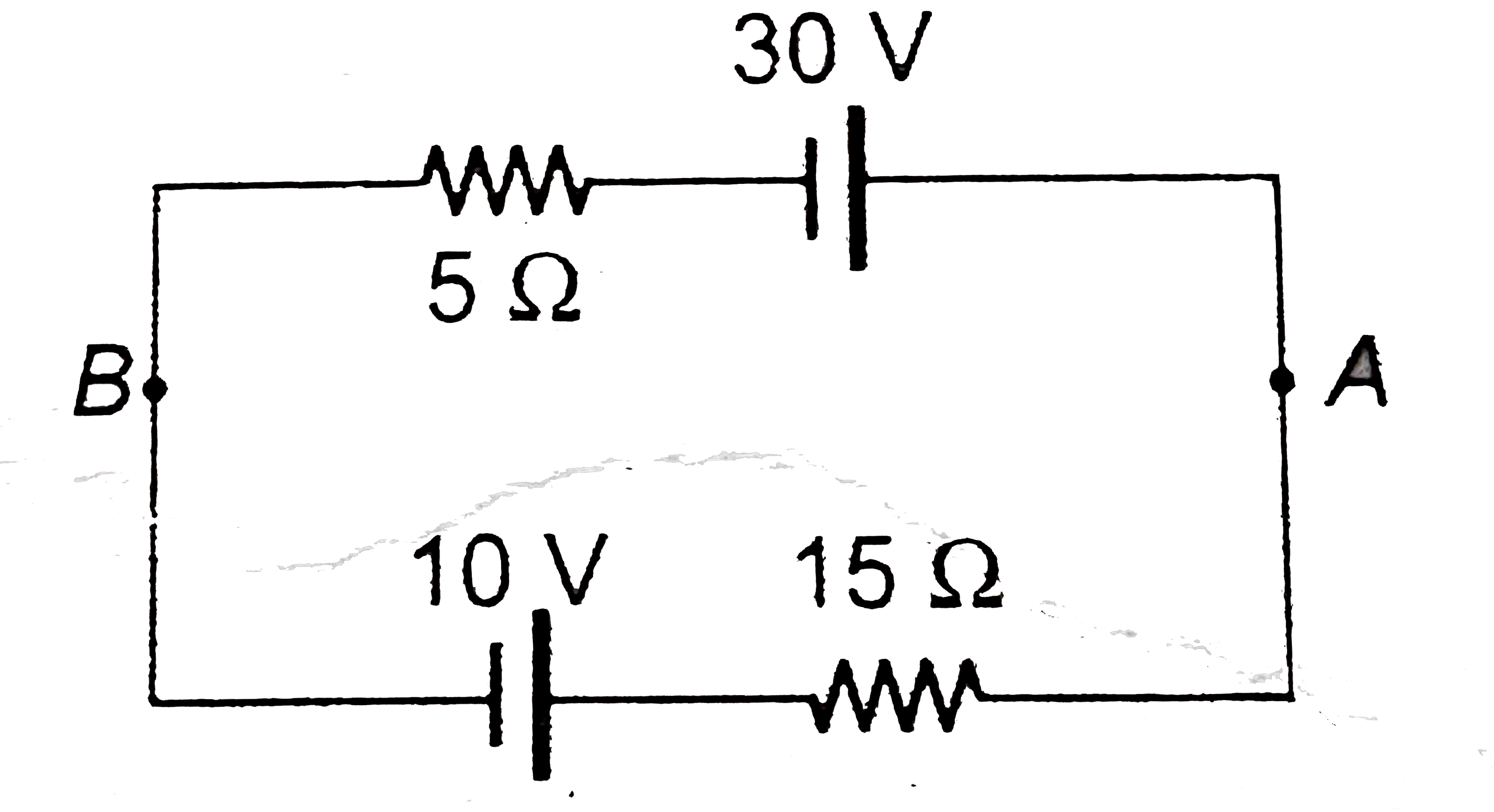
( e) Calculate the current in each resistor and terminal potential difference across each cell.

(f) Calculate potential difference across each cell.
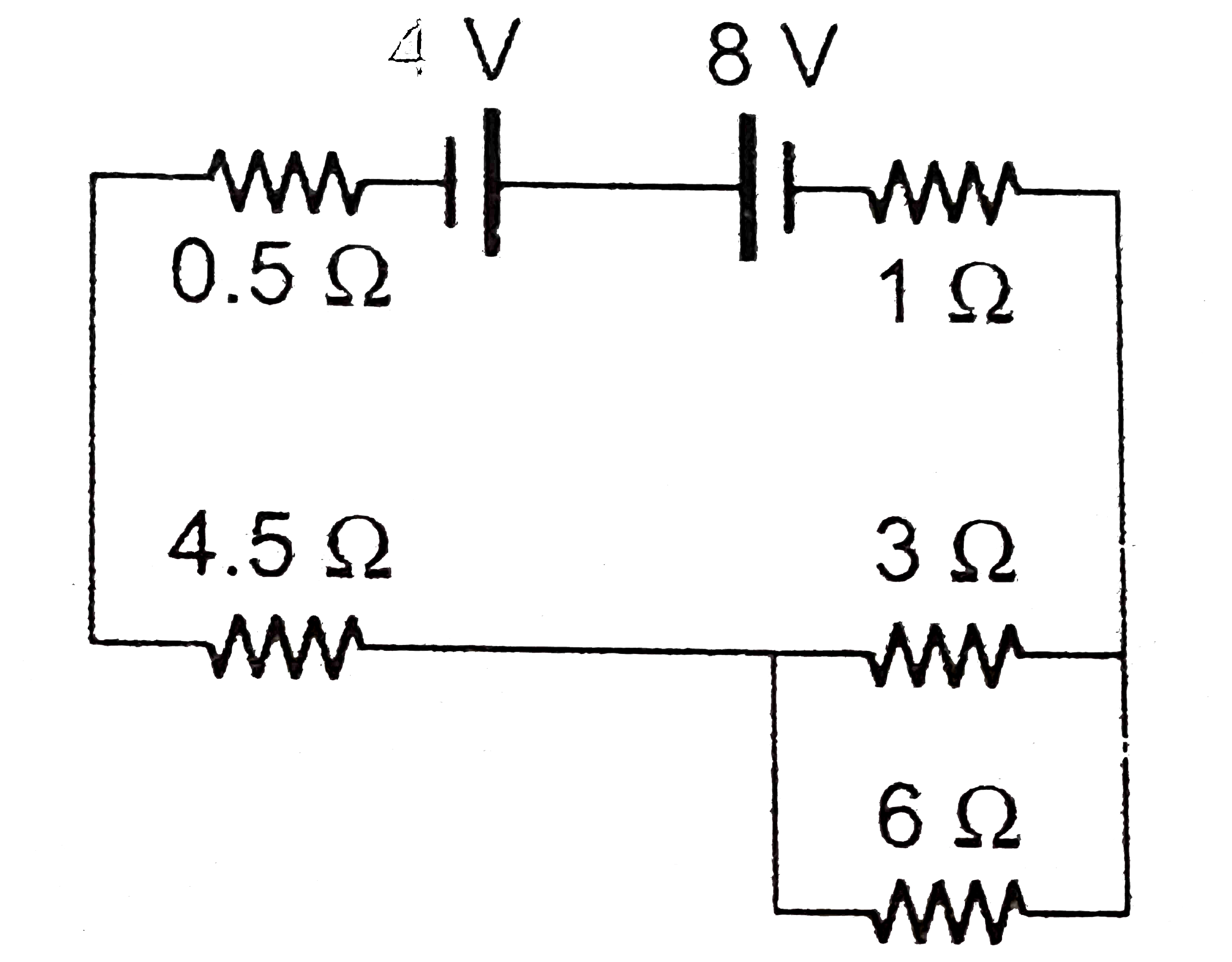
(g) A battery of 6 cells each of emf 2V and internal resistance 0.5Ω is being changed by DC mains of emf 220V by using an external resistance of 10Ω. Calculate.
(i) the charging current
(ii) the potential difference across the battery.
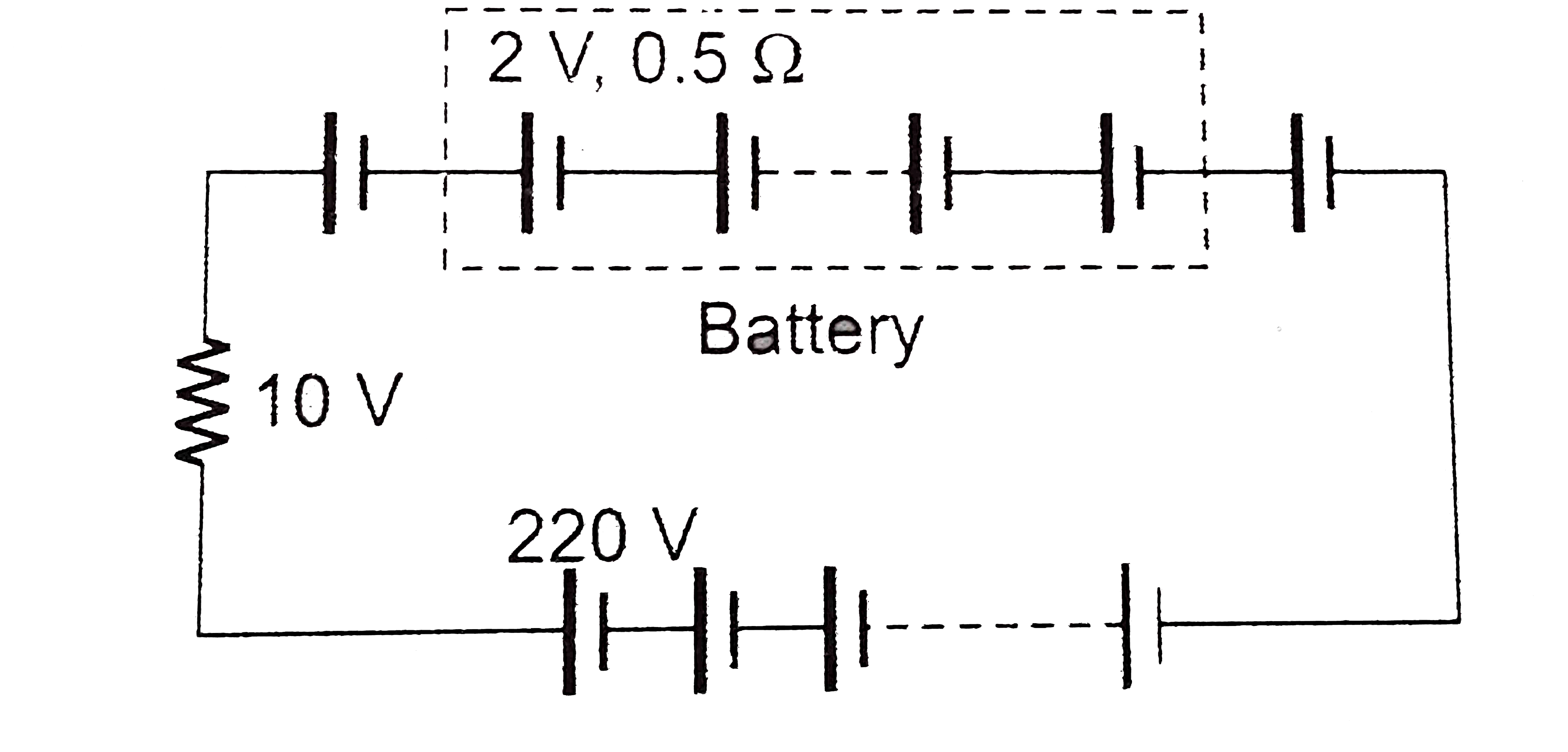 .
.
View SolutionA battery of six cells each of e.m.f . 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω. What is the potential difference across the battery?
View Solution
Knowledge Check
A battery of 20 cells (each having e.m.f. 1.8V and internal resistance 0.1Ω is charged by 220 volts and the charging current is 15A. Calculate the resistance to be put in the circuit.
A4m/sB10ms2C5ms2D2√2ms2A battery of emf 8 V with internal resistance 0.5Ω is being charged by a 120 V dc supply using a series resistance of 15.5Ω. The terminal voltage of the battery is
A20.5 VB15.5 VC11.5 VD2.5 VA cell of emf 1.5 V is connected with an external resistance 20Ω. The potential difference falls to 1.0 V. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0Ω
A battery of six cells each of e.m.f. 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω what will be the charging current.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionA set of 4 cell each of emf 2V and internal resistance 1.5Ω are connected across an external load of 10Ω with 2 rows, two cells in eacg row. Calculate the current in each row and potential difference across 10Ω
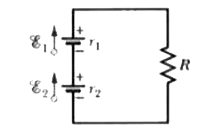
View SolutionIn Fig. 27-51. battery 1 has emf ε1=12.0V and internal resistance r1=0.025Ω and battery 2 has emf2=12.0V and internal resistance r2=0.012Ω. The batteries are connected in series with an external resistance R. (a) What R value makes the terminal-to-terminal potential difference of one of the batteries zero? (b) Which battery is that?
View SolutionA car battery with a 12V e.m.f. and an internal resistance of 0.04Ω is being charged with a current of 50A.
The potential difference V across the terminals of the battery are:
View Solution