Question

Two balls are thrown simultaneously, A vetically upwards with a speed of $20m{s}^{-1}$ from the ground, and B vetically downwards from height of 40 m with the same speed and along the same line of motion. At what points do the two balls collide? Take $g=9.8m{s}^{-2}$.

Options

A. 15 m above from the ground
B. 15 m below from the top of the tower
C. 20 m above from the ground
D. 20 m below fromt the top of the tower

Answer

A

Explanation

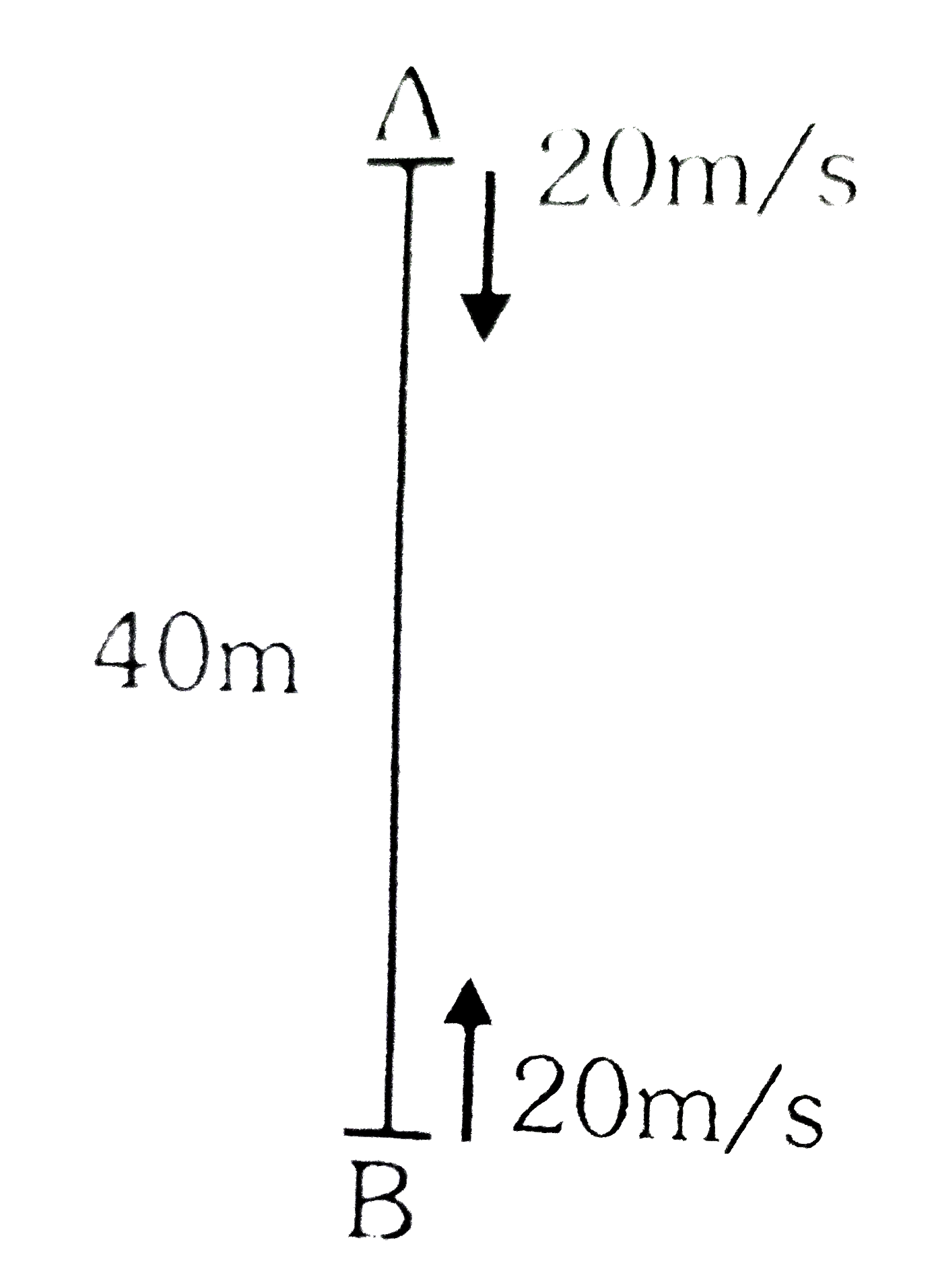
`u_(r)=20+20=40m//s`
`d_(1)=40`
`a_(rel)=g-g=0`
So using time of crossing
`=(d_(rel))/(u_(rel))=(40)/(40)=1` sec
Now for B, using `s=ut+(1)/(2)at^(2)`
`h=20xx1+(1)/(2)(-10)(1)^(2)=20-5`
=15 m above from ground