In vector diagram shown in figure where (→R) is the resultant of vectors (→A) and (→B). If R=B√2, the value of angle θ is :

A
30∘
B
45∘
C
60∘
D
75∘
Video Solution
Text Solution
The correct Answer is:B
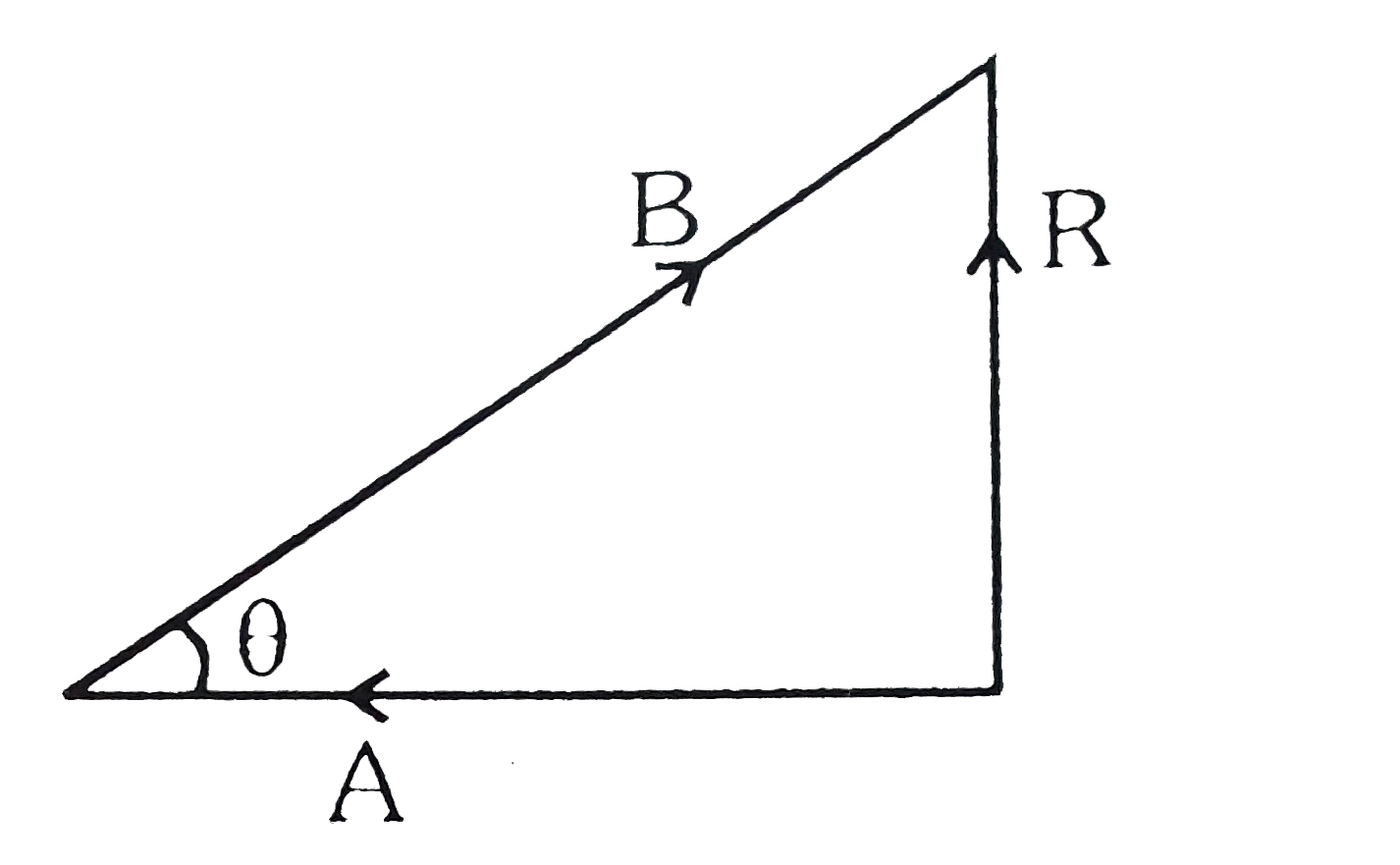
sinθ=R2=B/√2B=1√2⇒θ=45∘
|
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-3
20 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - UNIT & DIMENSIONS
19 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-1
128 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
In vector diagram shown in figure where (→R) is the resultant of vectors (→A)and(→B).
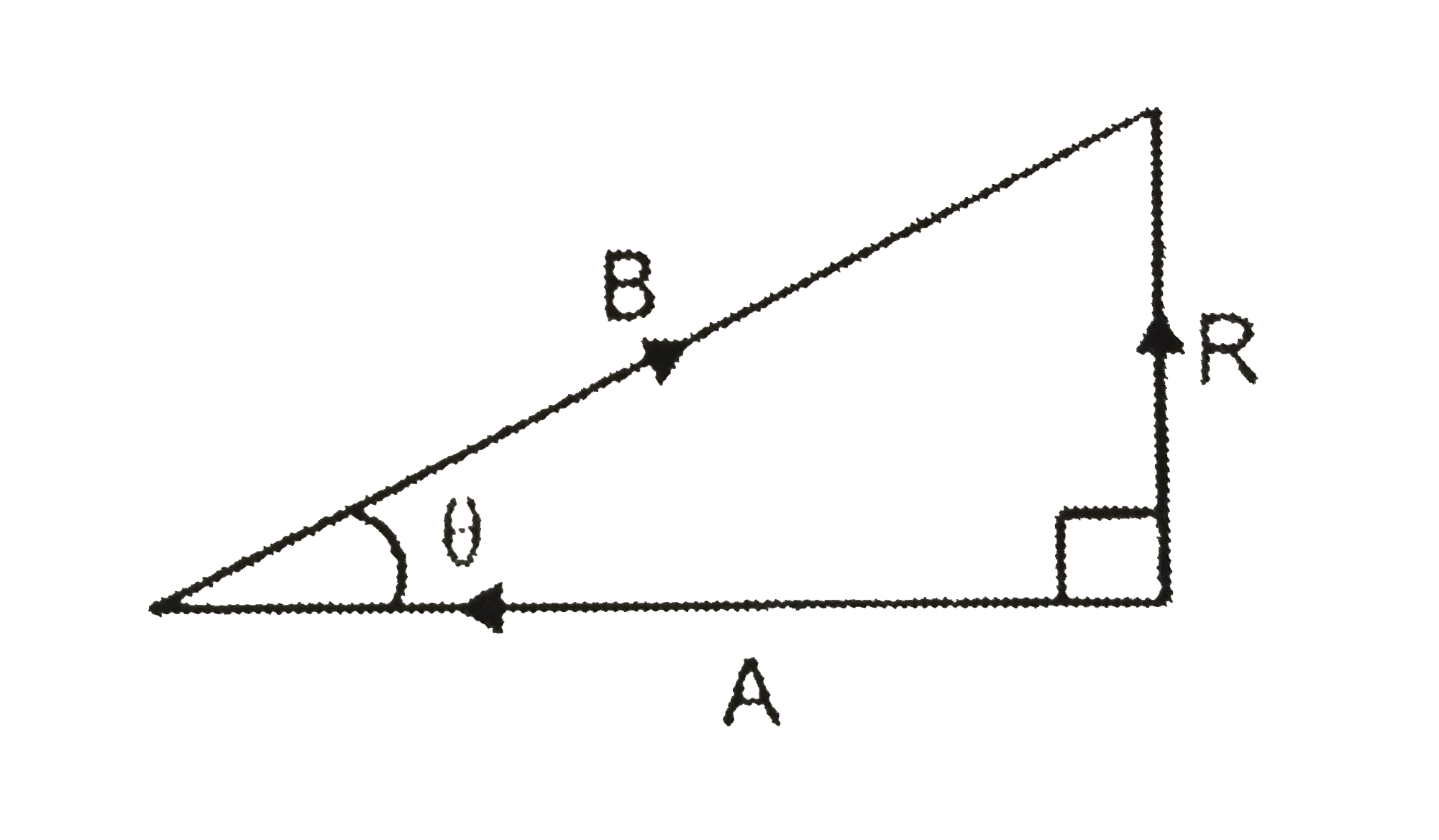
If R=B√2, then value of angle θ is :A30∘B45∘C60∘D75∘The vector sum of two vectors →Aand→B is maximum , then the angle θ between two vector is
A0∘B30∘C45∘D60∘The value of the sum of two vectors →A and →B with θ as the angle between them is
A√A2+B2+2ABcosθB√A∘−B2+2ABcosθC√A∘+B2−2ABsinθD√A2+B2+2ABsinθ
→R is the resultant of →A and →B . →R is inclined to →A at angle theat1 and to →B at angle θ2, then :
View SolutionThe angle between the vectors →Aand→B is θ. The value of →A(→A×→B) is -
View SolutionVectors →A,→Band→C are shown in figure . Find angle between
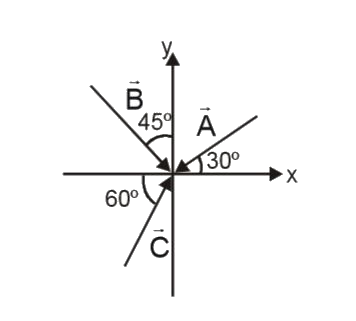
→Aand→B
View SolutionVector →R is the resultant of the vetors →Aand→B. Ratio of maximum value of ∣∣→R∣∣ to the minimum value of ∣∣→R∣∣ is 31. The ∣∣→A∣∣∣∣→B∣∣ may be equal to-
View Solution→Aand→B are two vectors and θ is the angle between them, if ∣∣→A×→B∣∣=√3(→A.→B) the value of θ is:-
View Solution
