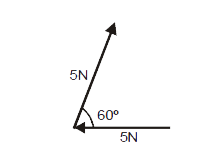
Two forces each numerically equal to 5N are acting as shown in the figure, then find resultant of these two vectors.
To find the resultant of two forces each numerically equal to 5N acting at an angle of 120 degrees to each other, we can use the vector addition formula for two vectors.
Given:
- Magnitude of each force, F1=F2=5N
- Angle between the forces, θ=120∘
We use the formula for the resultant of two vectors:
R=√F21+F22+2F1F2cosθ
1. Substitute the given values into the formula:
R=√52+52+2⋅5⋅5⋅cos120∘
2. Calculate the squares of the magnitudes:
R=√25+25+2⋅5⋅5⋅cos120∘
3. Calculate the cosine of 120 degrees:
cos120∘=−12
4. Substitute cos120∘ into the equation:
R=√25+25+2⋅5⋅5⋅(−12)
5. Simplify the expression inside the square root:
R=√25+25−25
6. Add the terms inside the square root:
R=√25
7. Calculate the square root:
R=5N
So, the resultant of the two forces is 5N.
- Magnitude of each force, F1=F2=5N
- Angle between the forces, θ=120∘
R=√F21+F22+2F1F2cosθ
R=√52+52+2⋅5⋅5⋅cos120∘
R=√25+25+2⋅5⋅5⋅cos120∘
cos120∘=−12
R=√25+25+2⋅5⋅5⋅(−12)
R=√25+25−25
R=√25
R=5N
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-1
128 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-2
80 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
Two forces, each numerically equal to 5 N, are acting as shown in the figure. Then the resultant is
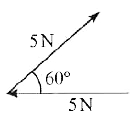 A2.5 NB5 NC5√3ND10 N
A2.5 NB5 NC5√3ND10 NTwo forces each numerically equal to 10 dynes are acting as shown in the following figure, then their resultant is -
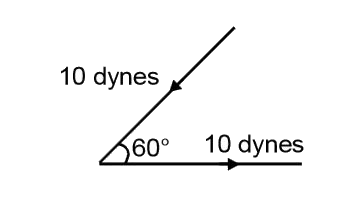 A10 dynesB20 dynesC10√3 dynesD5 dynes
A10 dynesB20 dynesC10√3 dynesD5 dynesTwo forces , each numerically equal to 10 dyne are acting as shown in the following figure Their resultant is :
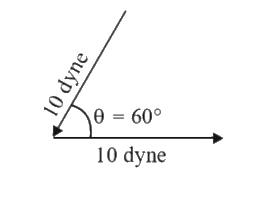 A10 dyneB20 dyneC10√3 dyneD5 dyne
A10 dyneB20 dyneC10√3 dyneD5 dyne
Find the resultant of the vectors shown in figure.

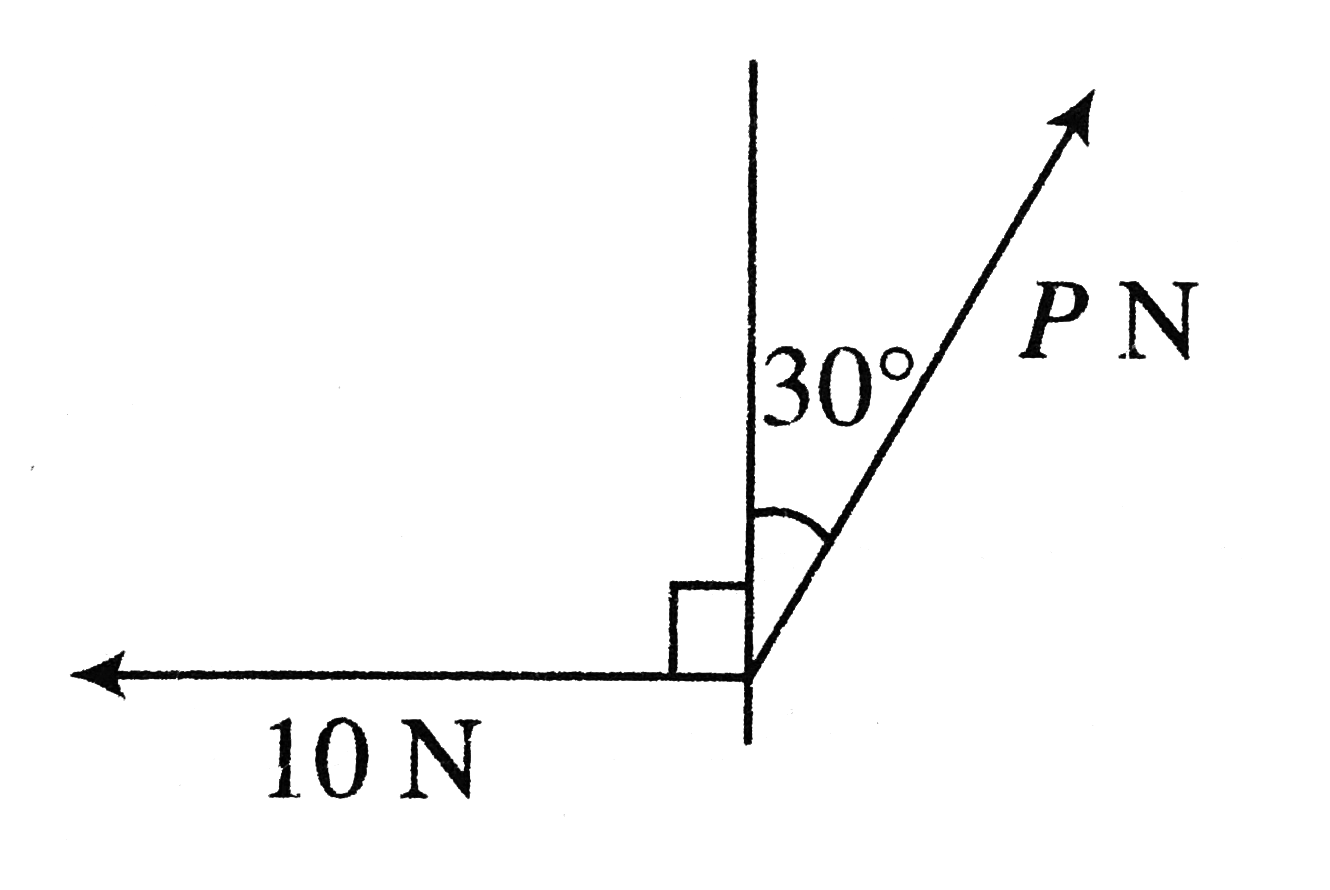
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
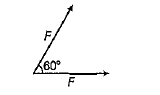
View SolutionTwo forces, each equal to F, act as shown in figure. Their resultant is
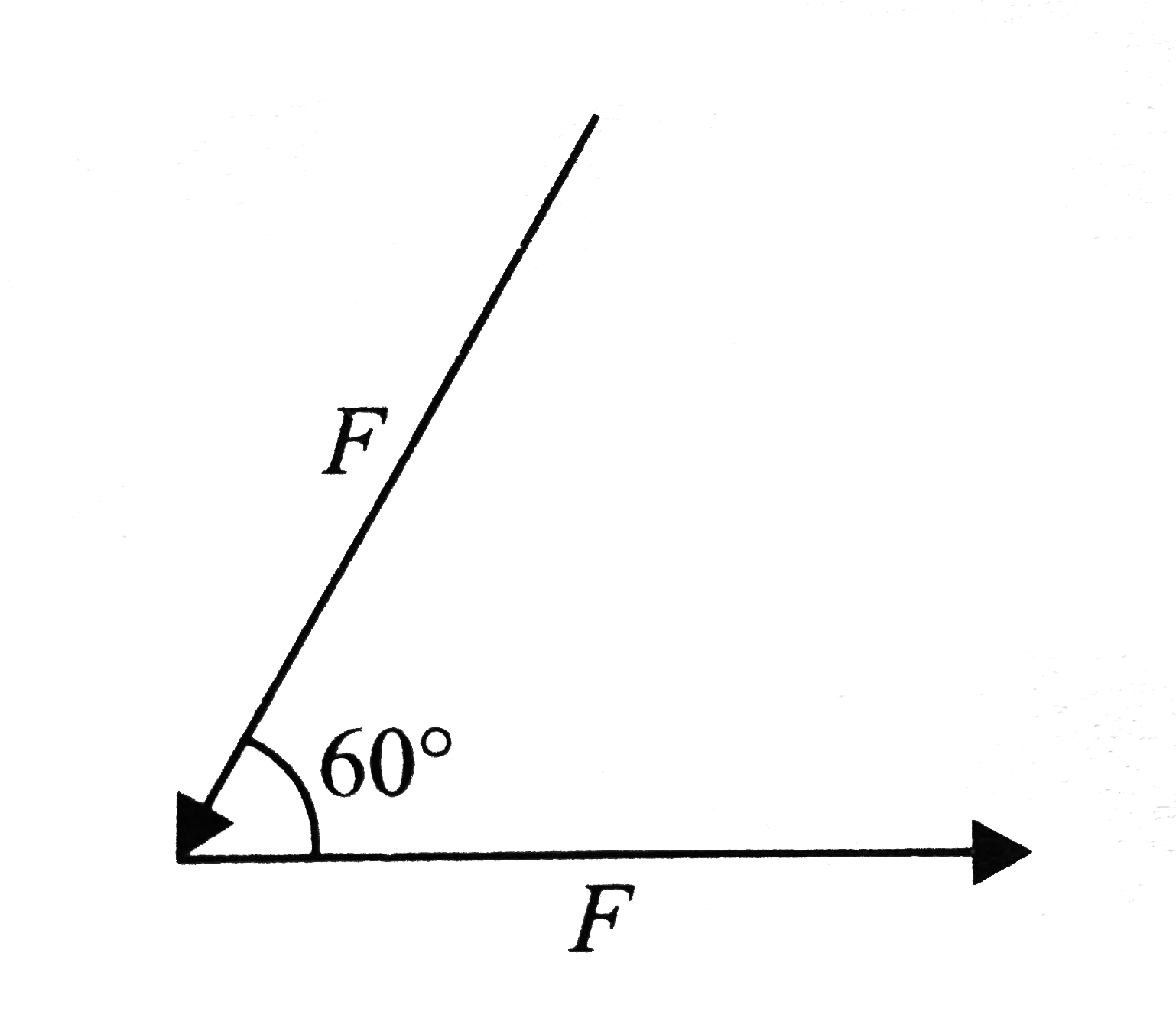
View SolutionTwo forces, each equal to F, act as shown in (figure) Their resultant is
View SolutionTwo forces 10 N and 15 N are acting on a body then which cannot be the resultant of these two forces
View Solution