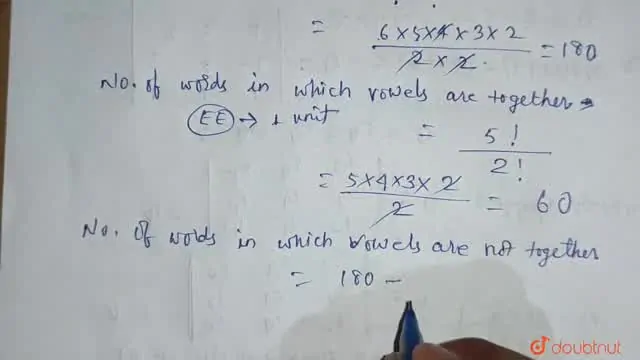The number of word (with or without meaning ) that can be formed from all the letter of the word " LETTER " in which vowels never come together is ______ .
Step by step video & image solution for The number of word (with or without meaning ) that can be formed from all the letter of the word " LETTER " in which vowels never come together is ______ . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
The number of words (with or without meaning that can be formed from all the letters of the word CORRONA in which vowels never come together is
View SolutionThe number of 4 letter words (with or without meaning) that can be formed from the letter of the work EXAMINATION is
View SolutionThe number of words with or without meaning that can be formed using all the letter of the words "FARMER" such that both R do not appear together is . .
View SolutionThe number of words from the letters of the words BHARAT in which B and H will never come together, is
View SolutionFind the number of different 4-leter words, with or without meaning, that can be formed from the letters of the word NUMBER.
View SolutionThe number of 4 letter words (with or without meaning) that can be formed from the eleven letters of the word ‘MATHEMATICS’ is _________.
View SolutionThe number of words from the letters of the words BHARAT in which B and H will never come together, is
View SolutionThe number of different words that can be formed from the letters of the word ‘INTERMEDIATE’ such that two vowels never come together is ________.
View SolutionThe number of six letter words (with or without meaning), formed using all the letters of the word 'VOWELS', so that all the consonants never come together, is____________
View SolutionThe number of different words that can be formed from the letters of the word ‘INTERMEDIATE’ such that two vowels never come together is ________.
View Solution