A battery of 3.0 V is connected to a resistor dissipating 0.5 W of power . If the terminal voltage of the battery is 2.5 V , the power dissipated within the internal resistance is :
0.072 W
0.125 W
0.50 W
0.10 W
To solve the problem step by step, we will analyze the given information and apply the relevant formulas.
1. Identify Given Values:
- EMF of the battery (E) = 3.0 V
- Terminal voltage (V) = 2.5 V
- Power dissipated in the external resistor (P_R) = 0.5 W
2. Calculate the Current (I):
The power dissipated in the external resistor can be expressed in terms of the current (I) and resistance (R) using the formula:
PR=I2R
We can also express the terminal voltage in terms of current and resistance:
V=IR
Rearranging gives us:
R=VI
Substituting this into the power equation gives:
PR=I2(VI)=IV
Therefore, we can find the current (I):
I=PRV=0.5 W2.5 V=0.2 A
3. Determine the Voltage Drop Across Internal Resistance (r):
The voltage drop across the internal resistance can be found using the formula:
E=V+Ir
Rearranging gives:
Ir=E−V
Substituting the known values:
Ir=3.0 V−2.5 V=0.5 V
4. Calculate the Power Dissipated in the Internal Resistance (P_r):
The power dissipated in the internal resistance can be calculated using:
Pr=I2r
From the previous step, we know:
r=IrI=0.5 V0.2 A=2.5 Ω
Now substituting this value into the power formula:
Pr=I2r=(0.2 A)2×2.5 Ω=0.04 A2×2.5 Ω=0.1 W
5. Final Answer:
Therefore, the power dissipated within the internal resistance is:
Pr=0.1 W
Summary of Solution:
The power dissipated within the internal resistance of the battery is 0.1 W.
---
- EMF of the battery (E) = 3.0 V
- Terminal voltage (V) = 2.5 V
- Power dissipated in the external resistor (P_R) = 0.5 W
The power dissipated in the external resistor can be expressed in terms of the current (I) and resistance (R) using the formula:
PR=I2R
We can also express the terminal voltage in terms of current and resistance:
V=IR
Rearranging gives us:
R=VI
Substituting this into the power equation gives:
PR=I2(VI)=IV
Therefore, we can find the current (I):
I=PRV=0.5 W2.5 V=0.2 A
The voltage drop across the internal resistance can be found using the formula:
E=V+Ir
Rearranging gives:
Ir=E−V
Substituting the known values:
Ir=3.0 V−2.5 V=0.5 V
The power dissipated in the internal resistance can be calculated using:
Pr=I2r
From the previous step, we know:
r=IrI=0.5 V0.2 A=2.5 Ω
Now substituting this value into the power formula:
Pr=I2r=(0.2 A)2×2.5 Ω=0.04 A2×2.5 Ω=0.1 W
Therefore, the power dissipated within the internal resistance is:
Pr=0.1 W
The power dissipated within the internal resistance of the battery is 0.1 W.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The power dissipated 6Ω resistor is
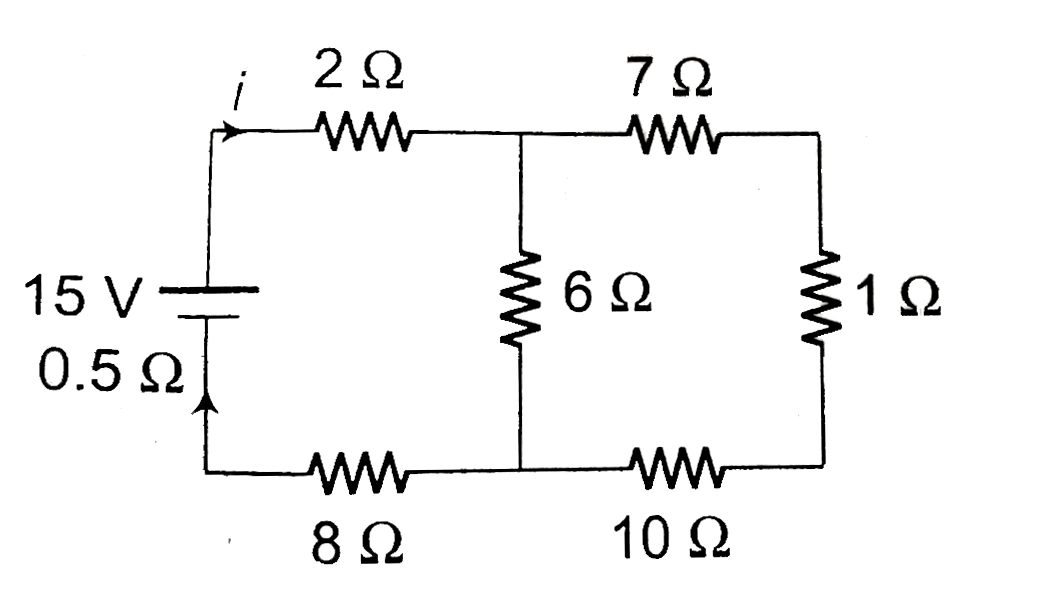 A278WB916WC616WD316W
A278WB916WC616WD316WA 50V battery is connected across a 10 ohm resistor. The current is 4.5 amperes. The internal resistance of the battery is
AZeroB0.5 ohmC1.1 ohmD5.0 ohmFive equal resistors when connected in series dissipated 5 W power. If they are connected in paralle, the power dissipated will be
A25 WB50 WC100 WD125 W
On giving 220 V to a resistor the power dissipated is 40 W then value of resistance is
View SolutionA battery of emf 10 V and internal resistance 3Ωis connected to a resistor. The current in the circuit is 0.5 A . The terminal voltage of the battery when the circuit is closed is
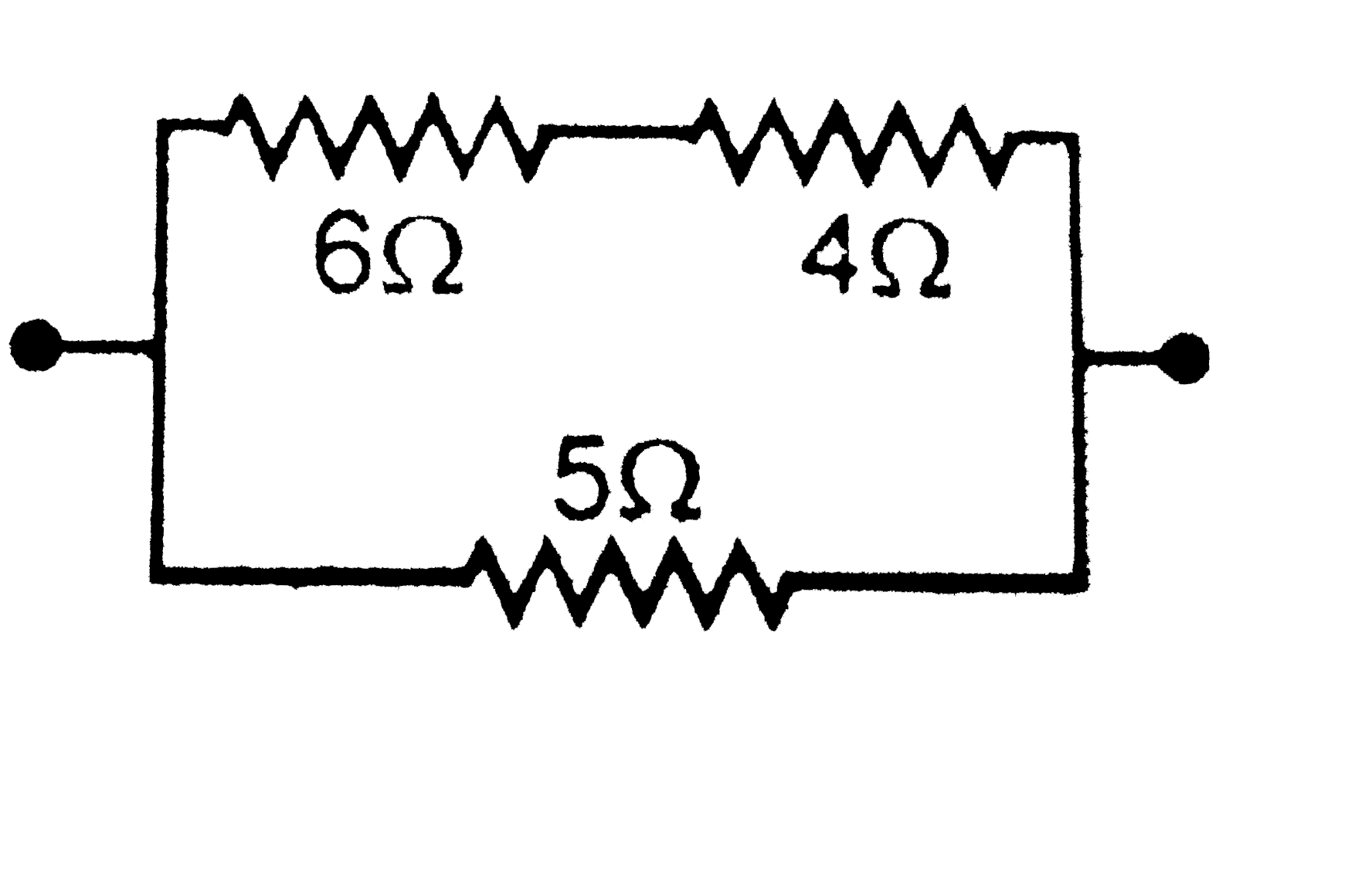
View SolutionIf the power dissipated in 5Ω is 20W then power dissipated in 4Ω is:-
View SolutionA battery when connected by resistance of 16Ω gives a terminal voltage of 12 V. and when connected by a resistance of 10Ω gives a terminal voltage of 11V. Then the emf of the battery ad its internal resistance
View SolutionA battery of e mf 10 V and internal resistance 3Ω is connected to a resistor as shown in the figure. If the current in the circuit is 0.5 A . then the resistance of the resistor will be
View Solution