In ________ arithmetic mean, all items of a series are given equal importance. (Simple/Weighted)
The correct Answer is:Simple
Step by step video, text & image solution for In ________ arithmetic mean, all items of a series are given equal importance. (Simple/Weighted) by Economics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANEXERCISE - EXERCISE ( C. State whether the following statements are True or False)8videos
MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEAN
- BOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANEXERCISE - EXERCISE ( D. Concept-based Objective Questions)16videos
MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEAN
- BOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANEXERCISE - Illustration72videos
MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEAN
- BOOK - TARUN JAIN & VK OHRICHAPTER - INDEX NUMBERSEXERCISE - NCERT Questions (With Hints to Answers)12videos
INDEX NUMBERS
- BOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF CENTRAL TENDENCY MEDIAN AND MODEEXERCISE - NCERT Questions (With Hints to Answers)5videos
MEASURES OF CENTRAL TENDENCY MEDIAN AND MODE
Similar Questions
Knowledge Check
- Question 1 - Select One
For calculating median , all items of the series are arranged in
Adescending orderBascending orderCasceneding or descending orderDNone of these - Question 2 - Select One
Arithmetic mean of these items 5,7,9,15,20 is:
A10B10.2C11.2D12 - Question 3 - Select One
Arithmetic mean of these items 5,7,9,15,20 is:
A10B10.2C11.2D12
Weighted Arithmetic Mean
View SolutionA student obtains the following percentage in an examination.
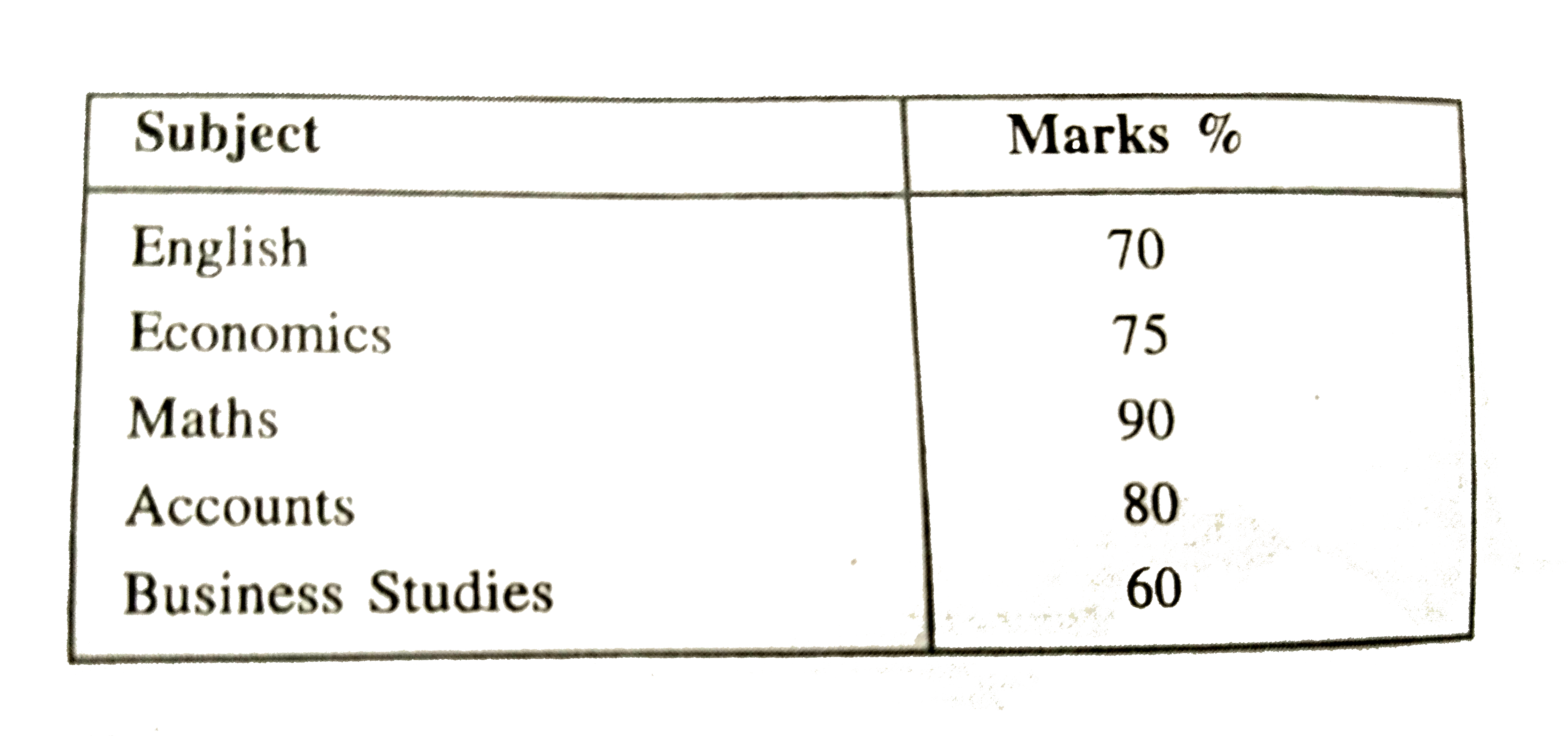
(i) Find out simple mean marks , if all subjectes are given equal weight.
(ii) Find out weighted mean marks, if the respective weights are 1,2,1,2,3View SolutionWeight of nine students of a class is given below. Calculate mean deviation, using median and arithmetic mean of the series. Also calculate coefficient of mean deviation:
Weight(kg): 47,50,58,45,53,59,47,60,49View SolutionArithmetic mean = (sum of all observations)/(Number of observations)
View SolutionThe arithmetic mean of the series 1,2,22,…….2n−1 is
View Solution

