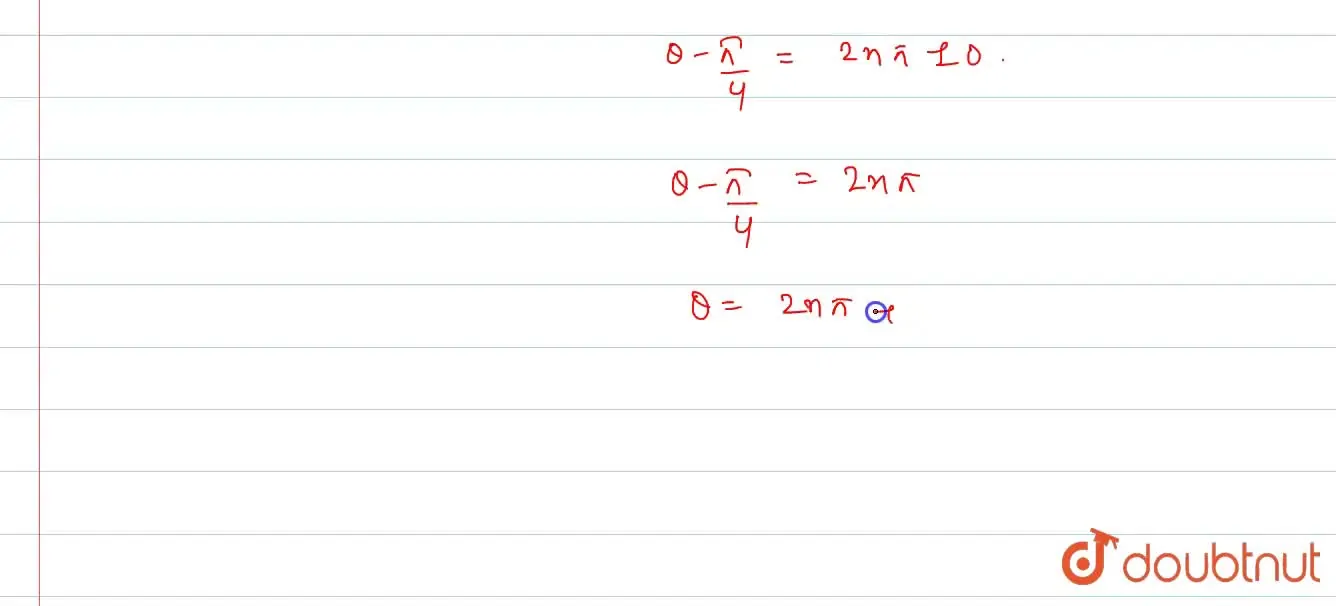sinθ+cosθ=√2
Video Solution
Text Solution
θ=2nπ+π4
|
Updated on:21/07/2023
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3M8videos
TRIGNOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3N36videos
TRIGNOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3K18videos
TRIGNOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - STRAIGHT LINESEXERCISE - Exercise206videos
STRAIGHT LINES
Similar Questions
If sinθ+cosθ=√2cosθ then what is (cosθ−sinθ) equal to ?
View SolutionEvaluate sinθ×cosθ if sinθ+cosθ=√2
View Solutionsinθ+cosθ=√3+12
View SolutionLet P={θ:sinθ−cosθ=√2cosθ}andQ={θ:sinθ+cosθ=√2sinθ} be two sets. Then
View SolutionLet P={θ:sinθ−cosθ=√2cosθ}andQ={θ:sinθ+cosθ=√2sinθ} be two ses. Then,
View SolutionIf sinθ+cosθ=√2cosθthencosθ−sinθ is equal to
View Solution∫(sinθ+cosθ)√sin2θdθ=
View Solution∫(sinθ+cosθ)√sin2θdthη is equal to
View SolutionIf cosθ−sinθ=√2sinθ, then prove that:
cosθ+sinθ=√2cosθView SolutionIf secθ(cosθ+sinθ)=√2 then what is the value of (2sinθ)(cosθ−sinθ) ?
View Solution