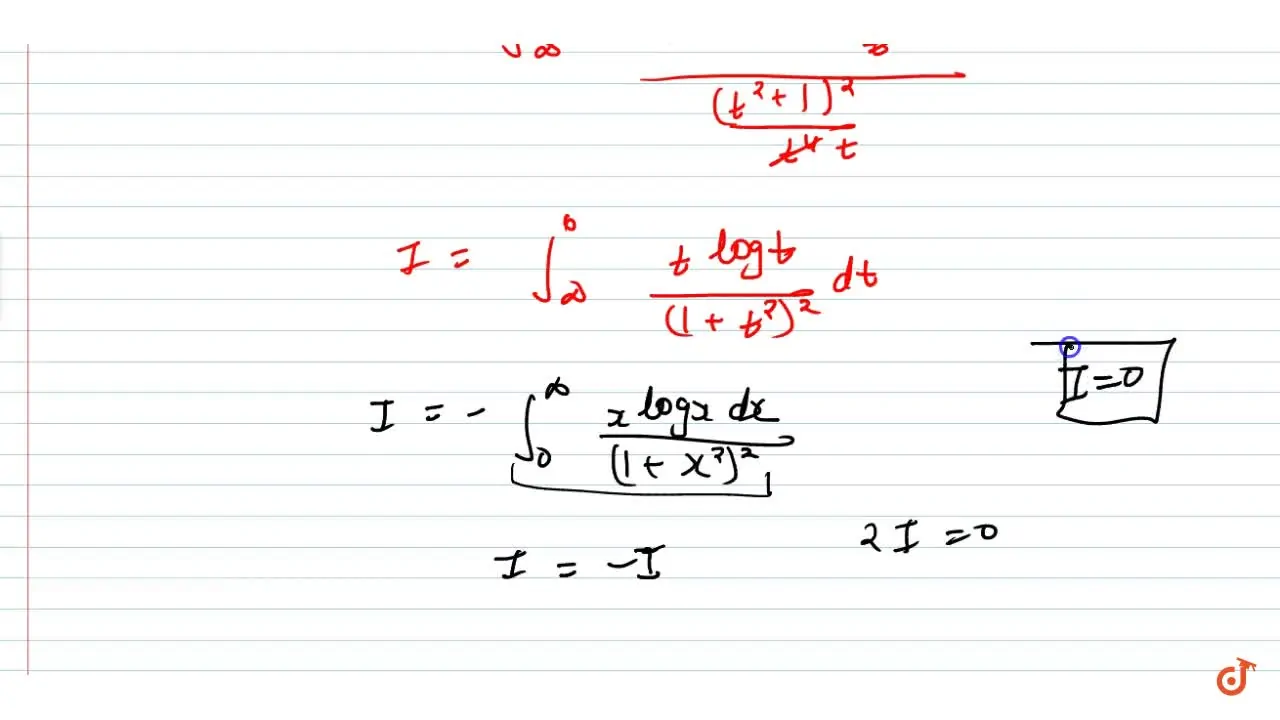The value of the integral ∫∞0xlogx(1+x2)2dxis 0 (b) log 7 (c) 5 log 13 (d) none of these
A
0
B
log7
C
5log13
D
none of these
Video Solution
Text Solution
I=∫∞0xlogxdx(1+x2)2
Let x=1t
∴I=∫0∞(1t)log(1t)(−1t2)dt(1+1t2)2
=−∫∞0tlogt(1+t2)2dt=−1
or I=0
|
Updated on:21/07/2023
Similar Questions
The value of the integral ∫∞0xlogx(1+x2)2dxis 0 (b) log 7 (c) 5 log 13 (d) none of these
View SolutionThe value of the integral ∫∞0xlogx(1+x2)2dx is
View SolutionThe value of the integral ∫∞0xlogx(1+x2)2dxis 0 (b) log 7 (c) 5 log 13 (d) none of these
View SolutionThe value of the integral ∫10logsin(πx2)dx is
View SolutionThe value of integral∫10log(1+x)1+x2dx, is
View SolutionThe value of the integral ∫π0xlogsinxdx is
View Solutionthe value of integral ∫20log(x2+2)(x+2)2dx is
View SolutionThe value of the integral ∫π/20log|tanx|dx is
View SolutionThe value of the integral ∫20log(x2+2)(x+2)2, dx is
View Solution" 8."int_(0)^(oo)(log x)/(1+x^(2))dx
View Solution