Let AandB be two 2×2 matrices. Consider the statements (i) AB=O⇒A=OorB=O (ii)AB=I2⇒A=B−1 (iii) (A+B)2=A2+2AB+B2 (i) and (ii) are false, (iii) is true (ii) and (iii) are false, (i) is true (i) is false (ii) and, (iii) are true (i) and (iii) are false, (ii) is true
Step by step video & image solution for Let Aa n dB be two 2xx2 matrices. Consider the statements (i) A B=O => A=O or B=O (ii)A B=I_2 => A=B^(-1) (iii) (A+B)^2=A^2+2A B+B^2 (i) and (ii) are false, (iii) is true (ii) and (iii) are false, (i) is true (i) is false (ii) and, (iii) are true (i) and (iii) are false, (ii) is true by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
(i)M is the brother of N
(ii) B is the brother of N,and
(iii)M is the brother of D, which of the following statements is definitely true?AN is the brother of BBN is the brother of DCM is the brother of BDD is the brother of M
(c−a) will be equal to 10(a+c) II. 10a+2b a. only I is true b. Only II is true c. Both I and II are true d. Both I and II are false
View SolutionIf A and B are two sets such that A(⊂)B then find : (i) A∪B (ii) A∩B (iii) A−B
View SolutionIn Figure, which of the following statements must be true? (i) a+b=d+c (ii) a+c+e=1800 (iii) b+f=c+e (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
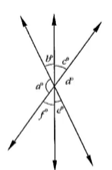 View Solution
View SolutionState True or False: ab>ba is true. If a=3 and b=4, but false if a=2 and b=3.
View SolutionIf sets A = (-3, 2] and B = (-1, 5], then find the following sets
(i) A∩B (ii) A∪B (iii) A−B (iv) B−AView Solution1. Strike out what is not true in the following.
b. Rajkumar Shukla was
(i) poor.
(ii) physically strong.
(iii) illiterate.View SolutionSubtract :
(i) −5y2 from y2
(ii) 6xy from -xy
(iii) (a−b) from (a+b)View Solution
