A uniform magnetic field B exist in a direction perpedicuar to the plane of a square loop made of a metal wire. The wire has diameter of 4 mm and a total length of 30 cm . The magnetic field changes with time at a steady rate dB/dt = 0.032 Ts−1 . The induced current in the loop is close to (Resistivity of the metal wire is 1.23×10−8Ωm)
0.53 A
0.34 A
0.61 A
0.43 A
Step by step video & image solution for A uniform magnetic field B exist in a direction perpedicuar to the plane of a square loop made of a metal wire. The wire has diameter of 4 mm and a total length of 30 cm . The magnetic field changes with time at a steady rate dB/dt = 0.032 T s^(-1) . The induced current in the loop is close to (Resistivity of the metal wire is 1.23 xx 10^(-8) Omega m) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
A uniform magnetic field B exists in a direction perpendicular to the plane of a square frame made of copper wire. The wire has a diameter of 2 mm and a total length of 40cm. The magntic field changes with time at a steady rate dBdt=0.02Ts−1.F∈dthecurrent∈duced∈theame.Resistivityofcopper=1.7 X 10 ^(-8) Wm.
View SolutionA uniform magnetic field B exists in a direction perpendicular to the palne of a square frame made of copper wire. The wire has a total length of 40cm . The magnetic field changes with time at a steady rate (dB/dt)=0.02T/sec . Find the current induced in the frame. Resistance of wire =I0Ω
View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
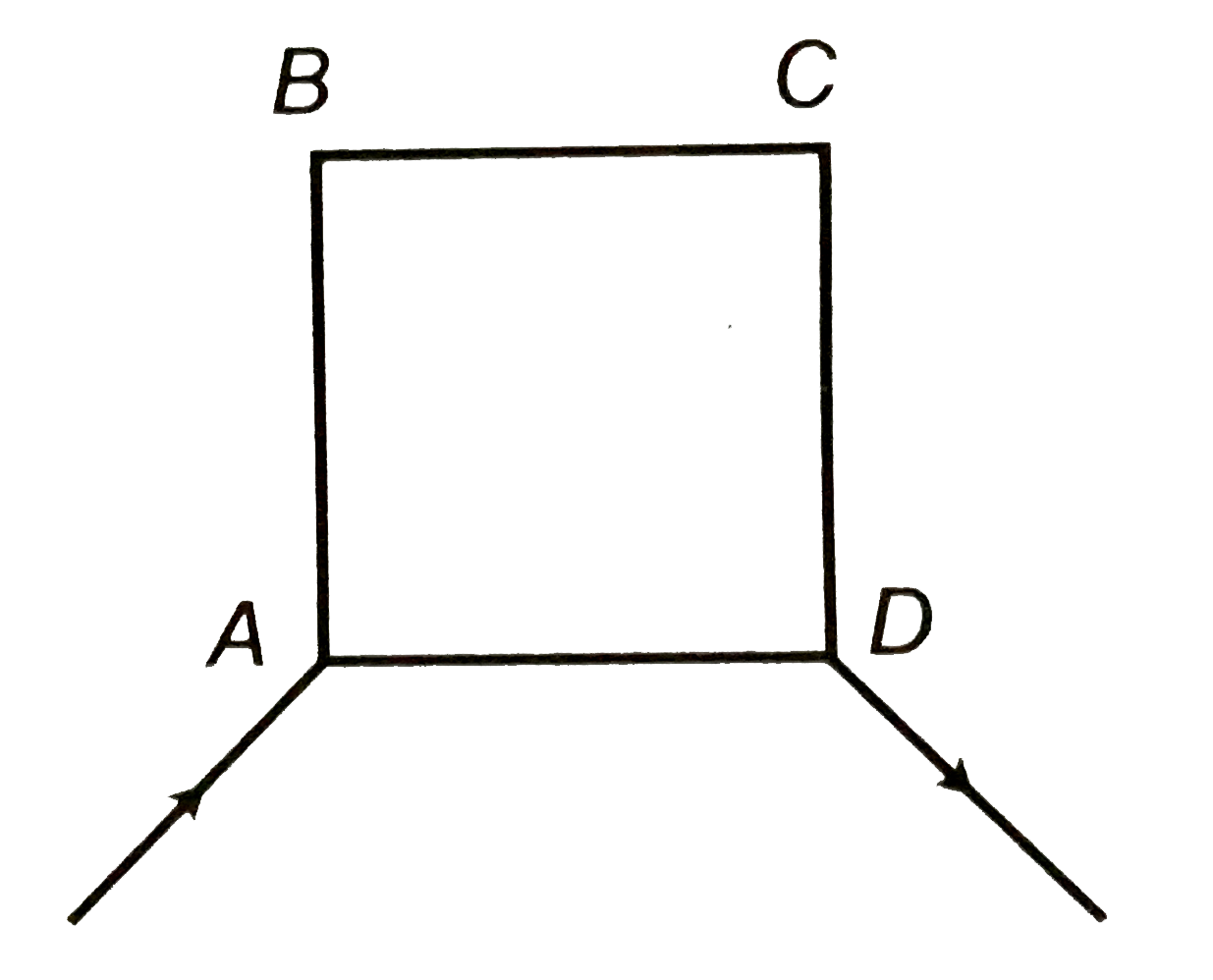 View Solution
View SolutionA square wire loop of side 30cm & wire cross section having diameter 4mm is placed perpendicular to a magnetic field changing at the rate 0.2 T/s. Final induced current in the wire loop.
(Given: Resistivity of wire material is (1.23×10−8ohmm)View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionMagnetic Field || Wire || Loop
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionFigure shows a square loop made from a uniform wire. If a battery is connected between the pionts A and C. What will be the magnetic field at the centre O of the square?
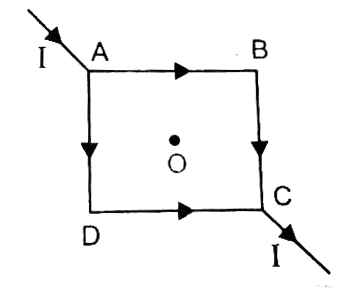 View Solution
View SolutionA square conductind loop, 20.0cm on a side placed in the same magnetic field as shown in Fig. 3.195, center of the magnetic field region, where dB/dt=0.035Ts−1.

he direction of induced electric field at points a, b and c:View Solution


