Let →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is correct ?
there is exactly one choice for such →v
there are infinitely many choices for such →v
if ˆu lies in the xy - plane then |u1|=|u2|
if ˆu lies in the xz-plane then 2|u1|=|u3|
The correct Answer is:B, C
b.,c.
|ˆu×→v|=1
⇒|→v|sinθ=1, whereθ is angle between ˆuand→v
also ˆw.(ˆu×→v)=1
⇒|ˆw||ˆu||ˆv|sinθcosα=1,where α is angle beteen ˆwand(ˆu×→v)
⇒1,1(1)cosα=1
⇒α=0
⇒ˆu×→v=λˆwwhere λ>0
⇒∣∣
∣
∣∣ˆiˆjˆku1u2u3v1v2v3∣∣
∣
∣∣=λ√6(ˆi+ˆj+2ˆk)
⇒(u2v3−u3v2)ˆi+(u3v1−u1v3)ˆj+(u1v2v1)ˆk=λ√6(ˆi+ˆj+2ˆk)
→v is a vector such that (ˆu×→v) is parallel to ˆw
u3=0⇒u2v3=λ√6and−u1v3=λ√6⇒|u2|=|u1|
u2=0⇒−u3v2=λ√6andu1v1=2λ√6⇒|u1|=2|u3|
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - single correct answer type
1 Video
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - multiple correct answers type
1 Video
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - chapter -3 multiple correct answers type
2 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank
24 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
Let →u=u1ˆi+u2ˆj be a unit vector in xy plane and →w=1√6(ˆi+ˆj+2ˆk) . Given that there exists a vector →c " in " R3 " such that |→u×→v|=1 and →w. (→u×→v)=1 , then
A|u1|=|u2|B|u2|=2|u2|C2|u1|=|u2|D|u1|−3|u2|Let →u=u1ˆi+u3ˆk be a unit vector in xz-plane and →q=1√6(ˆi+ˆj+2ˆk). If there exists a vector →v in such that |→u×→u|=1and→w.(→u×→c) .Then
A|u1|=|u3|B|u1|=2|u3|C|u1|=2|u3|D2|u1|=|u3|Let →u=2ˆi−ˆj+ˆk,→v=−3ˆj+2ˆk be vectors in R3 and →w be a unit vector in the xy-plane. Then the maximum possible value of |(→u×→v).→w| is-
A√5B√12C√13D√17
The figure given below shows the orientation of two vectors →uand→v in the xy plane .
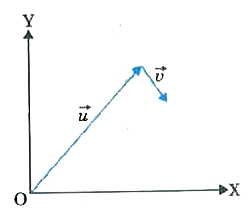
if →u=aˆi+bˆjand→v=pˆi+qˆj
Which of the following is correct ?
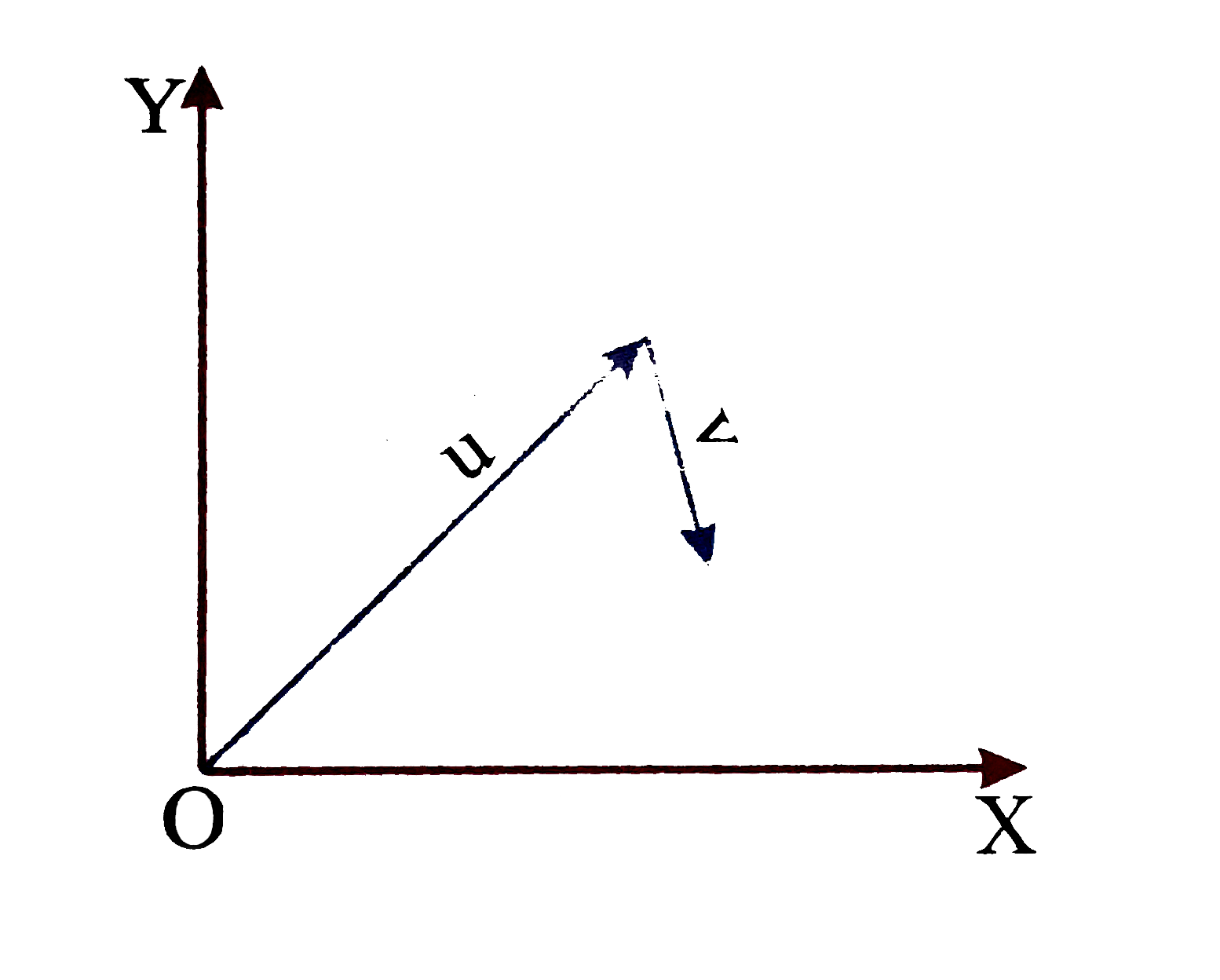
View SolutionFigure shows the orientation of two vectors u and vin the XY plane.
if→u=aˆi+bˆj and →v=pˆi+qˆj
which of the following is correct?
View SolutionThe unit vector parallel to the resultant vector of 2ˆi+4ˆj−5ˆkandˆi+2ˆj+3ˆk is
View SolutionFor three vectors, →u,→vand→w which of the following expressions is not equal to any of the remaining three ?
View SolutionLet →u=ˆi+ˆj,→v=ˆi−ˆjaandˆi−ˆjand→w=ˆi+2ˆj+3ˆk If ˆn isa unit vector such that →u.ˆn=0and→n.ˆn=0, then |→w.ˆn| is equal to
View Solution