A rod of length 2 units whose one ends is (1,0,−1) and other end touches the plane x−2y+2z+4=0, then which statement is false
the rod sweeps the figure whose volume is π cubic units.
the area of the region which the rod traces on the plane is 2π.
the length of projection of the rod on the plane is √3 units.
the centre of the region which the rod traces on the plane is (23,23,−53)
The correct Answer is:b
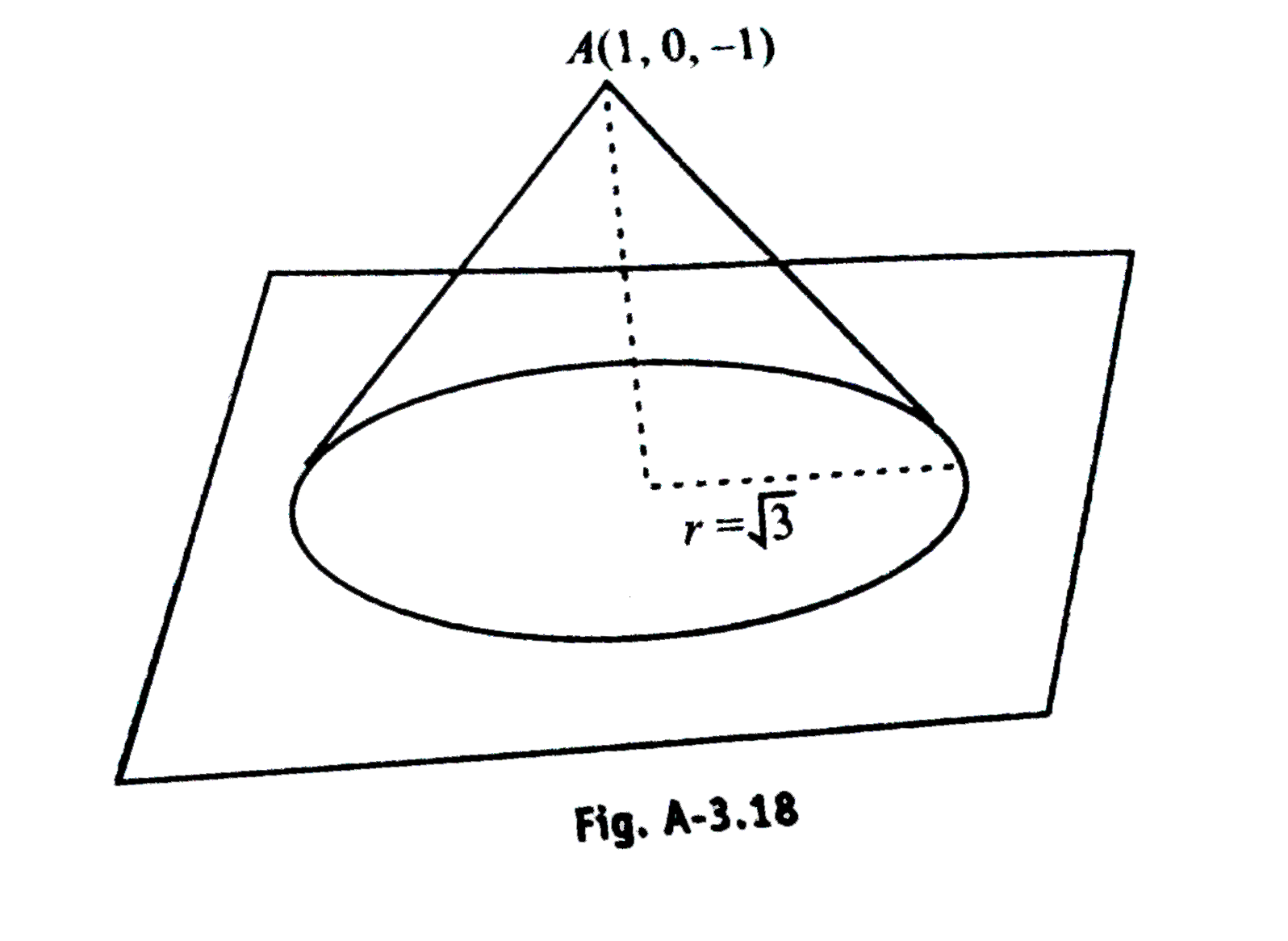
The rod sweeps out the figure which is a cone.
The distance of point A(1,0,−1) from the plane is
|1−2+4|√9=1 unit
The slant height l of the cone is 2 units.
Then the radius of the base of the cone is
√l2−1=√4−1=√3
Hence, the volume of the cone is
π3(√3)2⋅1=π cubic units
Area of the circle on the plane which the rod traces is 3π.
Also, the centre of the circle is Q(x,y,z). Then
x−11=y−0−2=z+12=−(1−0−2+4)12+(−2)2+22
or Q(x,y,z)≡(23,23,−53).
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Comprehension)
12 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Single)
86 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
Knowledge Check
A rod of length 2units whose one end is (1,0,−1) and other end touches the plane x−2y+2z+4=0, then
AThe rod sweeps the figure whose volume is ϕ cubic units.BThe area of the region which the rod traces on the plane is 2ϕ.CThe length of projection of the rod on the plane is √3 units.DThe centre of the region which the rod traces on the plane is (23,23,−53).The equation of the image of the plane x−2y+2z−3=0 in the plane x+y+z+1=0 is
Ax−8y+4z−7=0Bx−8y+4z−11=0Cx+8y−4z−7=0Dx+8y−4z−11=0The equation of the image of the plane x−2y+2z−3=0 in the plane x+y+z+1=0 is
Ax−8y+4z−7=0Bx−8y+4z−11=0Cx+8y−4z−7=0Dx+8y−4z−11=0
Find the equation of the image of the plane x−2y+2z−3=0 in plane x+y+z−1=0.
View SolutionWhat is the equation of the sphere which has its centre at (6,−1,2) and touches the plane 2x−y+2z−2=0 ?
View SolutionWhat is the equation of the sphere which has its centre at (6,-1,2) and touches the plane 2x−y+2z−2=0?
View SolutionA plane P passes through the line of intersection of the planes 2x−y+3z=2, x+y−z=1 and the point (1,0,1)
If the plane P touches the sphere x2+y2+z2=r2 then what is r equal to?
View SolutionThe equation of the plane which passes through
the points (2, 1, -1) and (-1, 3, 4) and
perpendicular to the plane x−2y+4z=0 is
View Solution
