Consider triangle AOB in the x−y plane, where A≡(1,0,0),B≡(0,2,0)andO≡(0,0,0). The new position of O, when triangle is rotated about side AB by 900 can be
(45,35,2√5)
(−35,√25,2√5)
(45,25,2√5)
(45,25,1√5)
The correct Answer is:c
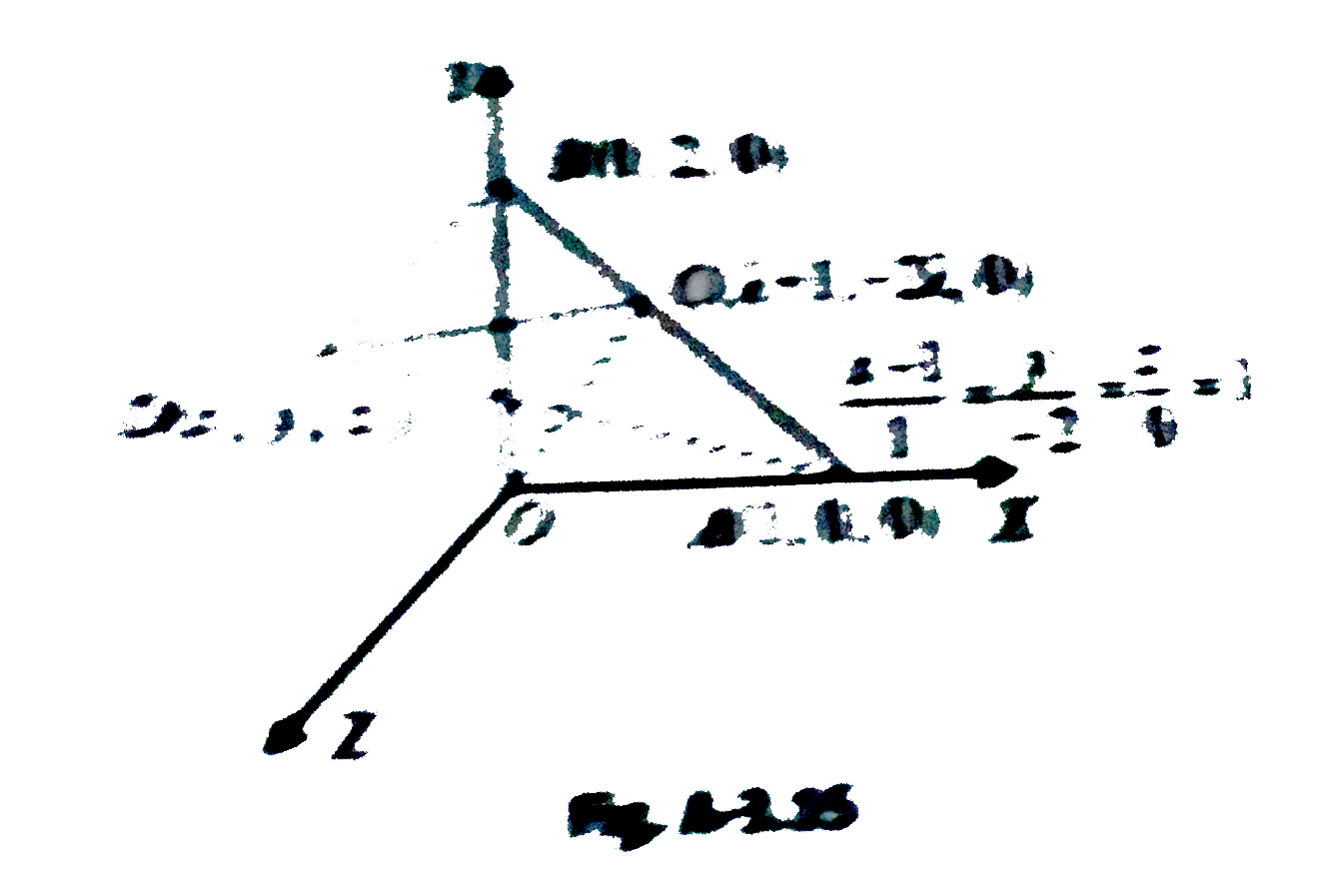
Equation of line AB is x−11=y−2=z0=λ
Now AB⊥OC⇒1(λ+1)+(−2λ)(−2)=0
or 5λ=−1orλ=−15
⇒ C is (45,25,0). Now
x21+(y1−2)2+z21=4 (i)
and (x1−1)2+y21+z21=1 (ii)
Now OC⊥CD
⇒ (x1−45)45+(y1−25)25+(z1−0)0=0 (iii)
From (i) and (ii), we get
−4y1+2x1=0orx1=2y1
From (iii), putting x1=2y1⇒2y1=45ory1=25⇒x1=(4)(5). Putting this value of x1andy1 in (i), we get
z1=±2√5
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Multiple)
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Subjective)
16 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
Consider triangle AOB in the x−y plane, where A≡(1,0,0),B≡(0,2,0)andO≡(0,0,0). The new position of O, when triangle is rotated about side AB by 900 can be a. (45,35,2√5) b. (−35,√25,2√5) c. (45,25,2√5) d. (45,25,1√5)
View SolutionWrite the equation of the plane passing through points (a, 0, 0), (0, b, 0)and (0, 0, c).
View Solution
Knowledge Check
The area of △AOB having vertices A(0,6),O(0,0) and B(6,0) is
A12 sq unitsB36 sq unitsC18 sq unitsD24 sq unitsThe orthocentre of the triangle with vertices O (0, 0). A(0,32),B(−5,0) is
A(52,34)B(−52,34)C(−5,32)D(0, 0)a and b are real numbers between 0 and 1 A(a,1),B(1,b)andC(0,0) are the vertices of a triangle.
If ∠C=90∘ thenAa+b=0Ba−b=0Ca+b=1Da−b=1
Consider the triangle OAB where O(0,0),B(3,4) ,if the orthocentre of a triangle is H(1,4) and co-ordinates of A is (a,b) ,then a+b
View SolutionWhat is the area of the triangle formed by the points O(0,0), A(4,0) and B(0,3)?
View Solution△ ABC with vertices A(0-2,0),B(2,0) and C(0,2) is similar to △ DEF with vertices D(-4,0) ,E(4,0) and F(0,4).
View SolutionWrite the perimeter of the triangle formed by the points O(0, 0), A(a, 0) and B(0, b) .
View SolutionThe area of ΔABC with vertices A(a, 0), O(0, 0) and B(0, b) in square units is
View Solution
