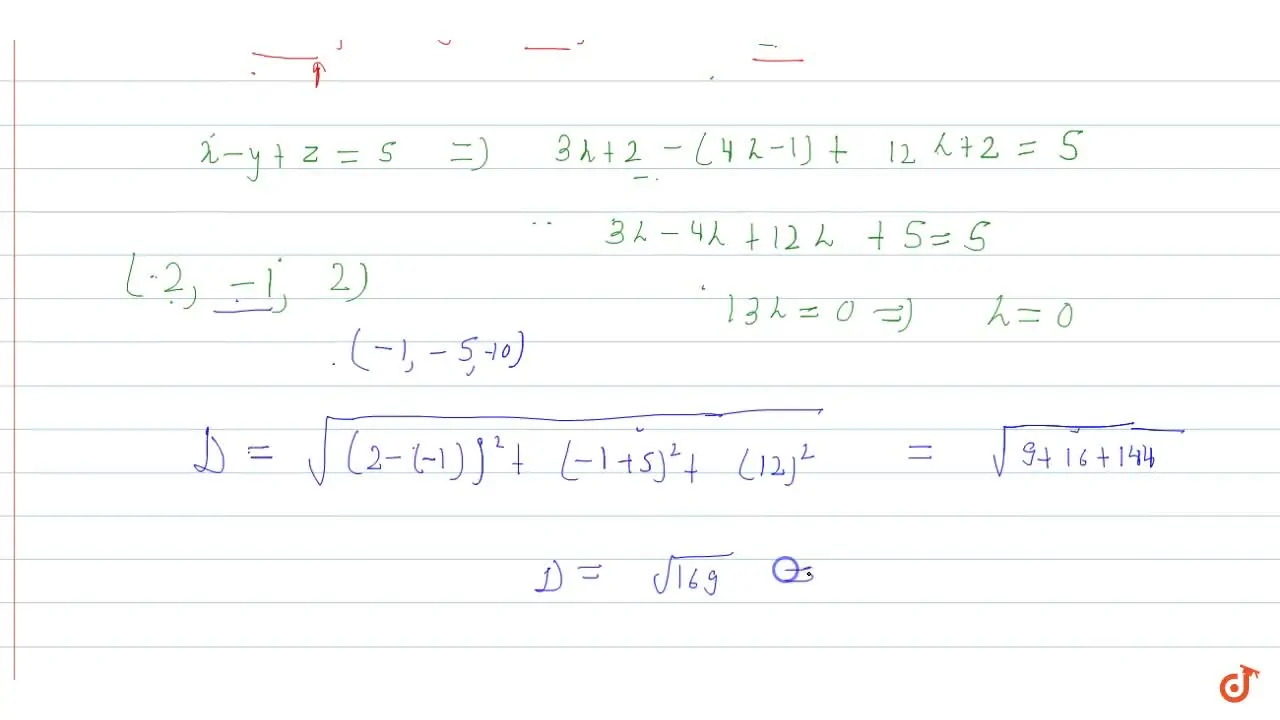Find the distance of the point (−1,−5,−10) from the point of intersection of the line x−23=y+14=z−212 and plane x−y+z=5.
Any point on the line x−23=y+14=z−212=λ is
(3λ+2,4λ−1,12λ+2).
This lies on x−y+z=5.
If 3λ+2−4λ+1+12λ+2=5orλ=0, then the point is (2,−1,2).
Its distance from (−1,−5,−10) is
√(2+1)2+(−1+5)2+(2+10)2
=√9+16+144=13
Related Playlists
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.45videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Subjective)16videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.215videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank34videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
Similar Questions
Find the distance of the points (−1,−5,−10) form the point of intersection of the line x−23=y+14=z−212 and plane x−y+z=5
View SolutionThe distance of the point (−1,−5,−10) from the point of intersection of the line x−22=y+14=z−212 and the plane x−y+z=5 is
View SolutionThe distance of the point (−1,−5,−10) from the point of intersection of the line x−22=y+14=z−212 and the plane x−y+z=5 is
View SolutionFind the distance of the point (−1,−5,−10) from the point of intersection of line x−23=y+14=z−22 and the plane x-y+z=5 measured parallel to the line x2=y3=z−6
View SolutionThe distance of the point (1, 0, 2) from the point of intersection of the line x−23=y+14=z−212 and the plane x y + z = 16, is : (1) 2√14 (2) 8 (3) 3√21 (4) 27
View SolutionThe disatance of the point (1,0,2) from the point of intersection of the line x−23=y+14=z−212 and the plane x−y+z=16, is
View SolutionFind the points of intersection of the line x−2−3=y−12=z−32 and the plane 2x+y−z=3.
View SolutionThe distance of the point (1,1,9) from the point of intersection of the line x−31=y−42=z−52 and plane x+y+z=17
View SolutionStatement 1: A point on the line x+23=y+12=z−32 at a distance 3√2 from the point (1,2,3) lies on the lne x+75=y+t4=z−21
Statement 2: If d is the distance between the point (−1,−5,−10) and the point of intersectionof the line x−23=y+14=z−212 with the plane x−y+z=5 then d=13View SolutionThe point of intersection of the line x−13=y+24=z−3−2 and the plane 2x−y+3z−1=0, is
View Solution