Find the number of solutions of the following equations: $x^{- \frac{1}{2}} {(log)}_{0.5} x = 1$ $x^{2} - 4 x + 3 - {(log)}_{2} x = 0$

Video Solution

Text Solution

Verified by Experts

(i) We have , $x^{- 1 / 2} {log}_{0.5} x = 1$
$\Rightarrow {log}_{0.5} x = \sqrt{x}$
To find the number of solutions, we must draw the graphs of $y = \sqrt{x} and y = {log}_{0.5} x$ and find the number of points of their intersection.
Graphs of functions are as shown in the following figure.

From the figure, we see that graphs intersect at only one point.
Hence, there is only one solution.
(ii) We have $x^{2} - 4 x + 3 - {log}_{2} x = 0$
or $x^{2} - 4 x + 3 = {log}_{2} x$
Let us draw the graphs of $y = x^{2} - 4 x + 3 and y = {log}_{2} x$ .

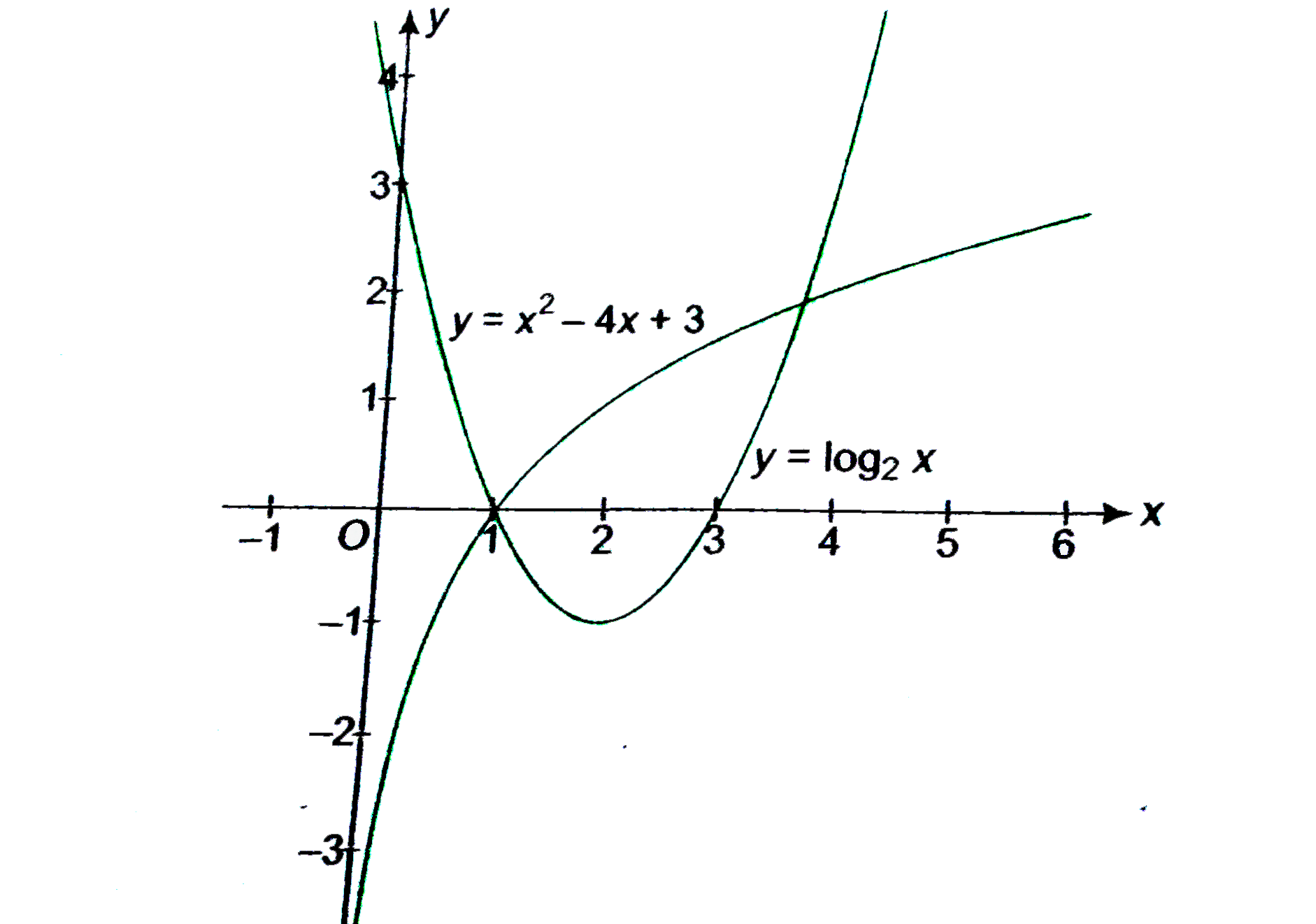
From the figure, we see that graphs intersect at two points.
Hence, there are two solutions.

Updated on:21/07/2023

The number of solutions of the equation
$x^{log {\sqrt{x}}^{2 x}} = 4$ is
A0
B1
C2
Dinfinitely many
The number of solution of the equation $log (- 2 x) = 2 log (x + 1)$ are
A $3$
B $2$
C $1$
D $0$
The number of solutions of the equation $2 x^{{log}_{10} x} + 3 x^{{log}_{10} (1 / x)} = 5$ is
A $1$
B $2$
C $3$
Dnone of these