A point moves so that the distance between the foot of perpendiculars from it on the lines $a x^{2} + 2 h x y + b y^{2} = 0$ is a constant $2 d$ . Show that the equation to its locus is $(x^{2} + y^{2}) (h^{2} - a b) = d^{2} {{(a - b)}^{2} + 4 h^{2}} .$

Video Solution

Text Solution

Verified by Experts

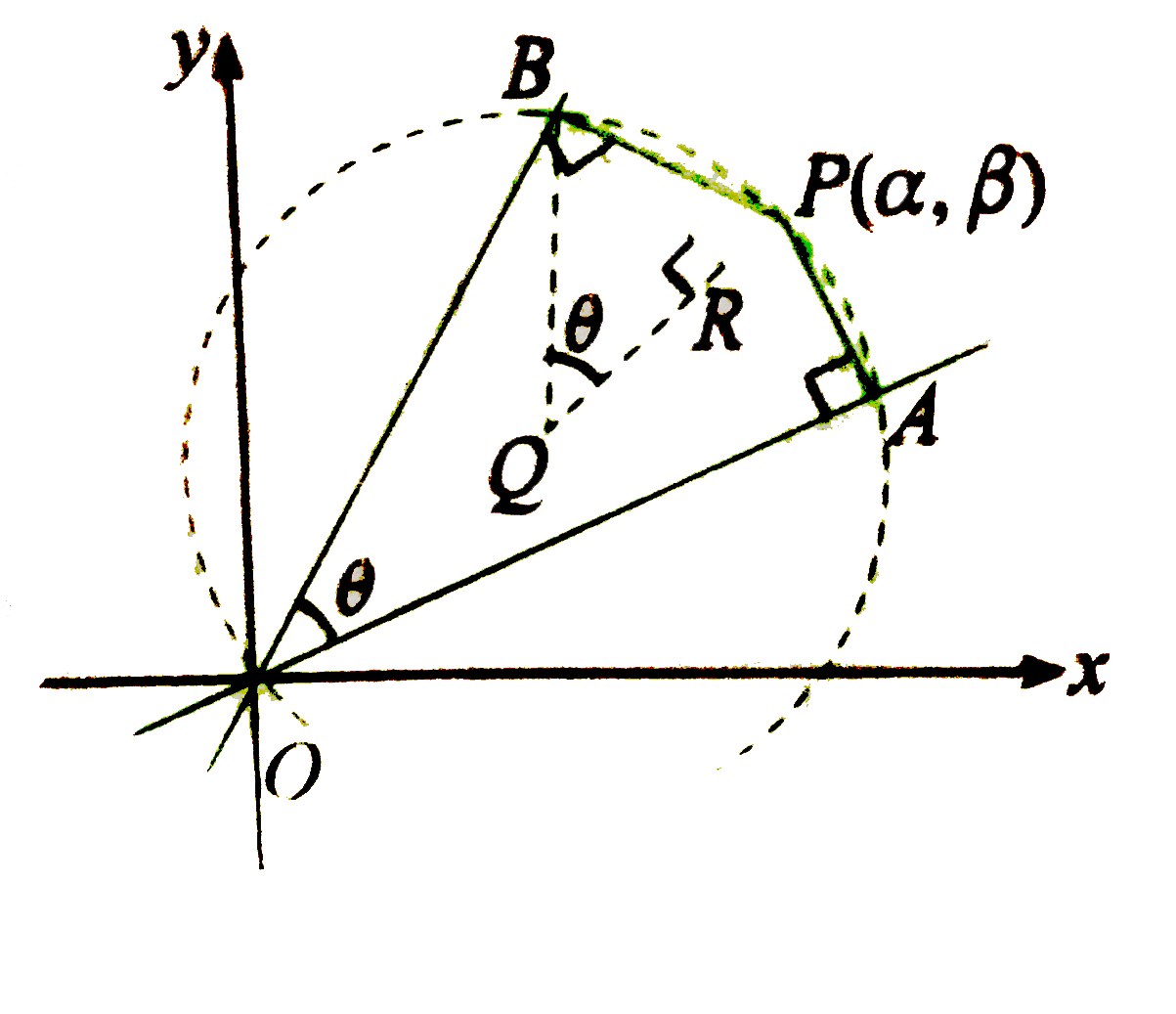
From point $p (α, β),$ perpendiculars are dropped on the given pair of lines.
According to the question , AB=2d. Clearly OAPB is a cyclic quadrilateral and OP will be the diameter of the circumcircle of this quadrilateral.
$O P = \sqrt{α^{2} + β^{2}}$
Let Q be the center of the circle.
therefore , in $Δ Q R B$ ,
$sin θ = \frac{B R}{Q B} = \frac{2 d}{\sqrt{α^{2} + β^{2}}}$ (1)
Also , angle between the lines is
$tan θ = \frac{2 \sqrt{h^{2} - b}}{a + b}$ (2)
Therefore , from (1) and (2), we get
$\frac{2 \sqrt{h^{2} - a b}}{a + b} = \frac{2 d}{\sqrt{α^{2} + β^{2} - 4 d^{2}}}$
Therefore , the locus of $P (α, β)$ is
$(x^{2} + y^{2}) (h^{2} - a b) = d^{2} {{(a - b)}^{2} 4 h^{2}}$

Updated on:21/07/2023

The locus of the foot of the perpendicular from the centre of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ on any tangent is given by ${(x^{2} + y^{2})}^{2} = l x^{2} + m y^{2}$ , where
A $l = a^{2}, m = b^{2}$
B $l = b^{2}, m = a^{2}$
Cl=m=a
Dl=m=b
The locus of the foot of the perpendicular drawn from the centre upon any tangent to the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , is
A ${(x^{2} + y^{2})}^{2} = a x^{2} + b y^{2}$
B $(x^{2} + y^{2}) = a^{2} x^{2} + b^{2} y^{2}$
C ${(x^{2} + y^{2})}^{2} = a^{2} x^{2} + b^{2} y^{2}$
DNone of the above
The locus of foot of perpendicular from focus of ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ to its tangents is
A $x^{2} + y^{2} = a^{2} + b^{2}$
B $x^{2} + y^{2} = a^{2}$
C $x^{2} + y^{2} = {(a + b)}^{2}$
Dnone of these