Two sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
same as that of B
opposite to that of B
θ=tan−1(12)→x−aξs
θ=tan−1(−12)→thex−aξs
The correct Answer is:(4)
According to the law of conservation of linear momentum along x - axis, we get
m1×0+m2×v=m1vcosθ
m2v=m1vcosθ
orcosθ=m2vm1v−−−−(i)
According to law of conservation of linear momentum along y - axis, we get
m1×0+m2×0=m1vsinθ+m2v2
−m2v2=m1vsinθ
sinθ=−m2v2m1v ....(ii)
Divide (ii) by (i) , we get
tanθ=−12
or θ=tan−1(−12) to the x-axis
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -II (H.W)
Explore 75 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
Two balls A and B of masses 0.3 kg and 0.2 kg respectively are moving along positive X-axis and negaive X-axis with velocities 2.0 m / s. They collide and thereafter move in the directions opposite to their original directions. Find the velocities of A and B after collision. Also, calculate total K.E. of the ball before and after collision.
View SolutionA ball moving with a velocity 12m/s strikes an identical ball at rest.After collision both balls move in directions making 300 with original direction of motion.speeds of the balls after collision are (in ms−1) ?
View Solution
Knowledge Check
Two spheres a and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the x-axisDθ=tan−1(−12) to the x-axisTwo spheres A and B of masses m1andm2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v2direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the axisDθ=tan−1(−12) to the x-axisA mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
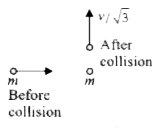
View SolutionA body of mass m moving at a constant velocity v hits another body of the same mass moving with a velocity v/2 but in the opposite direction and sticks to it. The common velocity after collision is
View Solution

