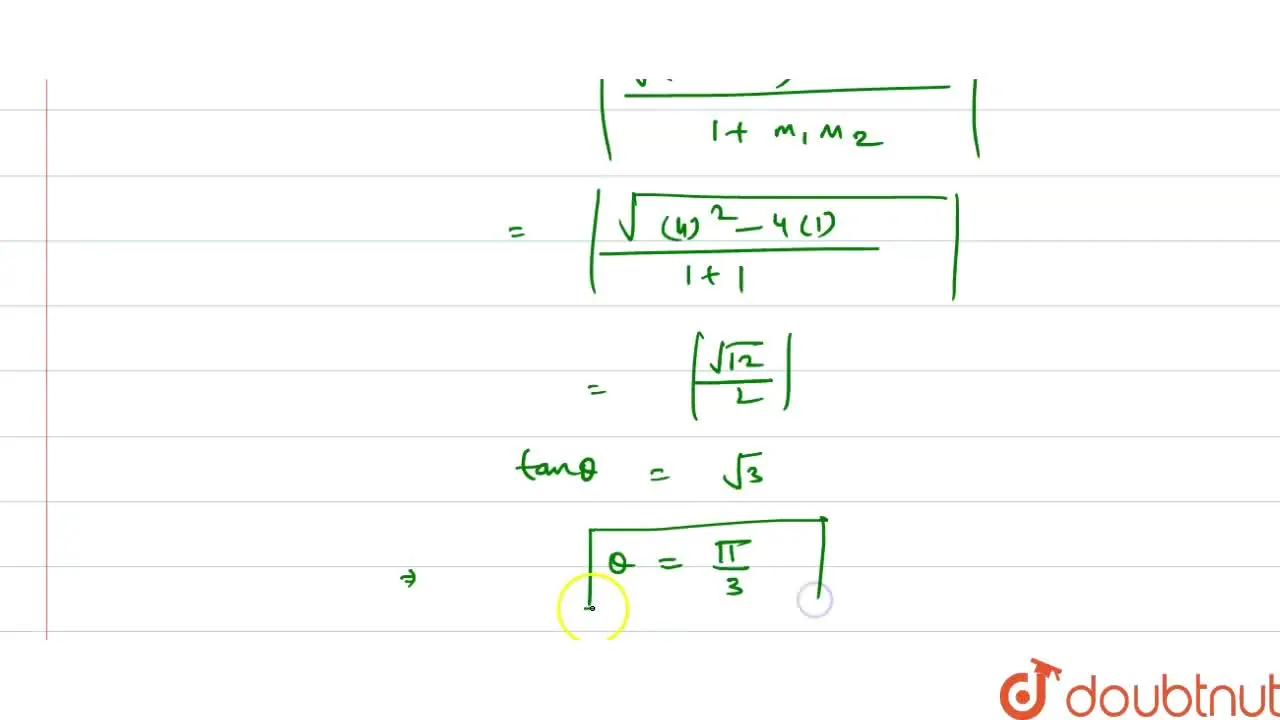The angle between the tangents drawn from the point (2, 6) to the parabola y2−4y−4x+8=0 is
π2
π4
π3
π6
The correct Answer is:C
Step by step video, text & image solution for The angle between the tangents drawn from the point (2, 6) to the parabola y^(2)-4y-4x+8=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
The angle between the tangents drawn from the point (1,4) to the parabola y2=4x is
View SolutionThe angle between the tangents drawn from the point (4, 1) to the parabola x2=4y is
View SolutionThe angle between the tangents drawn from the point (1, 4) to the parabola
y2=4x isView SolutionThe angle between the tangents drawn form the point (3, 4) to the parabola y2−2y+4x=0, is
View SolutionAngle between tangents drawn from the point (1,4) to the parabola y2=4x is
View SolutionThe angle between the tangents drawn from the point (1, 4) to the parabola y2=4x is (A) π6 (B) π4 (C) π3 (D) π2
View SolutionThe angle between the tangents drawn from the origin to the parabola y2=4a(x−a) is
View SolutionThe angle between the tangents drawn from the origin to the paraboala y2=4a(x−a), is
View SolutionAngle between the tangents drawn from the point (0 2020) to the parabola (y−2)2=(x−1)
View SolutionThe angle between tangents from the from the point (-1 ,-1) to the parabola y2=4x is
View Solution