Gravitational force acts on a particle due to fixed uniform solid sphere. Neglect other forces. Then particle
always moves normal to the radial direction.
always moves in the radial direction only.
always moves in circular orbit.
experiences a force directed along the radial direction only.
The correct Answer is:D
To solve the problem regarding the gravitational force acting on a particle due to a fixed uniform solid sphere, we can analyze the situation step by step.
1. Understanding the System:
- We have a fixed uniform solid sphere and a particle located at some point outside or on the surface of the sphere.
- The gravitational force exerted by the sphere on the particle acts towards the center of the sphere.
2. Direction of the Gravitational Force:
- The gravitational force is a central force, which means it always acts along the line joining the center of the sphere and the particle. This line is referred to as the radial direction.
3. Movement of the Particle:
- The problem states that we should neglect other forces acting on the particle, so we only consider the gravitational force.
- The particle can move in various ways: it can move in a straight line, in an elliptical path, or in a circular path depending on its initial velocity and position.
4. Analyzing the Options:
- Option 1: Suggests the particle moves normal to the radial direction. This is incorrect because if the particle were to move in a circular path, it would require a centripetal force directed towards the center, which is provided by the gravitational force. However, the particle can also move in a straight line.
- Option 2: States that the particle moves only in the radial direction. This is misleading because while the force is radial, the particle's motion can be in various directions depending on its initial conditions.
- Option 3: Claims the particle is moving in a circular orbit. This is not necessarily true as the particle can also move in a straight line or an elliptical path.
- Option 4: Correctly states that the particle experiences a force directed along the radial direction only. This is true as the gravitational force acts towards the center of the sphere.
5. Conclusion:
- The correct answer is Option 4, which states that the particle experiences a force directed along the radial direction only.
- We have a fixed uniform solid sphere and a particle located at some point outside or on the surface of the sphere.
- The gravitational force exerted by the sphere on the particle acts towards the center of the sphere.
- The gravitational force is a central force, which means it always acts along the line joining the center of the sphere and the particle. This line is referred to as the radial direction.
- The problem states that we should neglect other forces acting on the particle, so we only consider the gravitational force.
- The particle can move in various ways: it can move in a straight line, in an elliptical path, or in a circular path depending on its initial velocity and position.
- Option 1: Suggests the particle moves normal to the radial direction. This is incorrect because if the particle were to move in a circular path, it would require a centripetal force directed towards the center, which is provided by the gravitational force. However, the particle can also move in a straight line.
- Option 2: States that the particle moves only in the radial direction. This is misleading because while the force is radial, the particle's motion can be in various directions depending on its initial conditions.
- Option 3: Claims the particle is moving in a circular orbit. This is not necessarily true as the particle can also move in a straight line or an elliptical path.
- Option 4: Correctly states that the particle experiences a force directed along the radial direction only. This is true as the gravitational force acts towards the center of the sphere.
- The correct answer is Option 4, which states that the particle experiences a force directed along the radial direction only.
Topper's Solved these Questions
Similar Questions
The gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
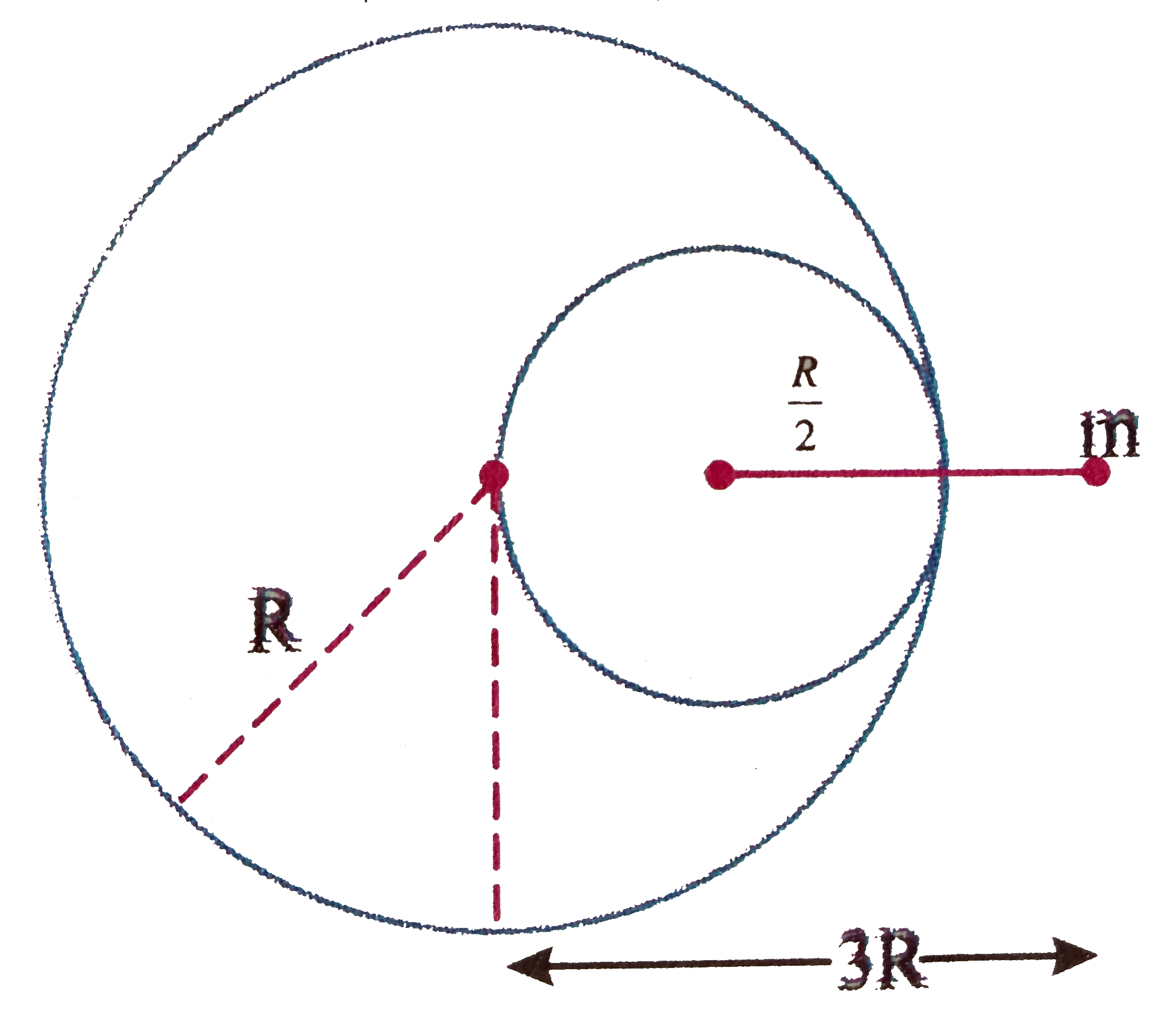
View SolutionDemonstrate that the gravitational force acting on a particle A inside a uniform spherical layer of matter is equal to zero.
View Solution
Knowledge Check
Gravitational field due to a solid sphere
Aremains constant throughout the sphereBincrease inside the sphere and decreases outside the sphereCincreases throughout with distance from the centerDdecreases throughout with distance from the centreFour forces acting on a particle keep it in equilibrium, then :-
Athe force must be coplanar.Bthe force cannot be coplanarCthe forces may or may not be coplanar.Dif three of these forces are coplanar, so must be the fourth.Assertion: The gravitational force on a particle inside a spherical shell is zero.
Reason: The shell shields other bodies outside it form exerting gravitational forces on a particle inside.AIf both the assertion and reason are true and reason is a true explantion of the assertion.BIf both the assertion and reason are true but the reason is not true the correct explantion of the assertion.CIf the assertion is true but reason falseDIf both the assertion and reason are false.
If a constant force acts on a particle, its acceleration will
View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
View SolutionStatement -1: Gravitational force between two particles is negligibly small compared to the electrical force.
Statement-2 :The electrical force is experienced by charged particles only.
View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
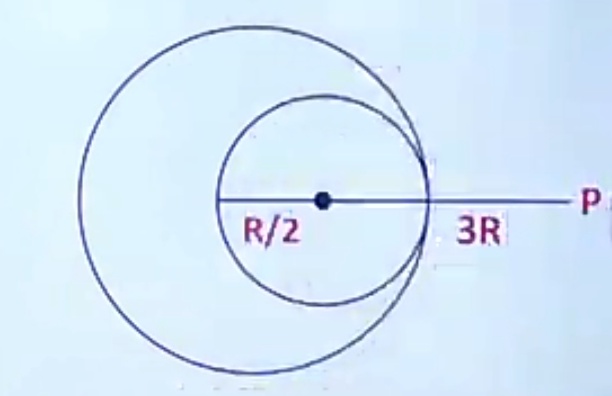
View SolutionThe centripetal force acting on a particle in UCM is proportional to
View Solution

