For a simple pendulum, the graph between T2andL (where T is the time period & Lis the length) is
A straigth line passing through the origin
Parabola
Circle
ellipse
The correct Answer is:A
Step by step video, text & image solution for For a simple pendulum, the graph between T^(2) and L (where T is the time period & Lis the length) is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (H.W)
19 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - III
29 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - I (H.W)
66 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
The time period of a simple pendulum is given by the formula, T=2π√l/g, where T = time period, l = length of pendulum and g = acceleration due to gravity.
If the length of the pendulum is decreased to 1/4 of its initial value, then what happens to its frequency of oscillations ?
View SolutionThe time period of a simple pendulum is given by the formula, T=2π√l/g, where T = time period, l = length of pendulum and g = acceleration due to gravity.
If the length of the pendulum is decreased to 1/4 of its initial value, then what happens to its frequency of oscillations ?
View Solution
Knowledge Check
For a simple pendulum the graph between length and time period will be
AhyperbolaBparabolaCstraight lineDnone of theseThe l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
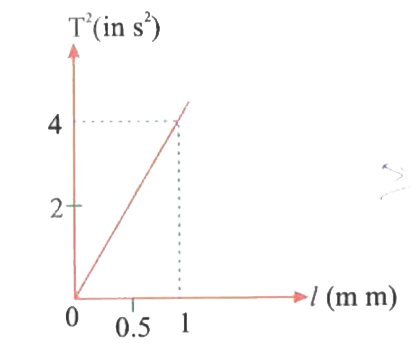 A1sB1.2 sC√2 sD1√2s
A1sB1.2 sC√2 sD1√2sTime period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about one end and oscillating in vertical plane is T2. Amplitude of oscillation in both the cased is small. The T1/T2 is:
A√2/√3B1/√3C√3/√2D1/√2
The graph between the length and square of the period of a simple pendulum is a
View SolutionTime period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is T2. Amplitude of osciallations in both the cases is small. Then T1T2 is
View SolutionA simple pendulum of length l1 has a time period of 4 s and another simple pendulum of length l2 has a time period 3 s. Then the time period of another pendulum of length (l1−l2) is
View SolutionThe time period of a simple pendulum in a stationary train is T. The time period of a mass attached to a spring is also T. The train accelerates at the rate 5 ms−2. If the new time periods of the pendulum and spring be TpandTs, respectively. Then,
View SolutionThe time period of a simple pendulum in a stationary train is T. The time period of a mass attached to a spring is also T. The train accelerates at the rate 5m/s2. If the new time periods of the pendulum and spring be TP and TS respectively, then :-
View Solution
