Two masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
√Km2,m1gK
√Km1,m2gK
√Km2,m2gK
√Km1,m1gK
The correct Answer is:A
Removed mass gives amplitude m1g=kA⇒A=m1gk
remaining mass gives frequency ω=√km2
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - I (H.W)
Explore 66 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - II (C.W)
Explore 27 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:C. U . Q
Explore 75 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
Two mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
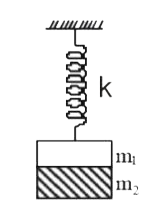
View Solution
Knowledge Check
Two masses m1 and m2 are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m1 is removed. Frequency and amplitude of oscillation of m2 are
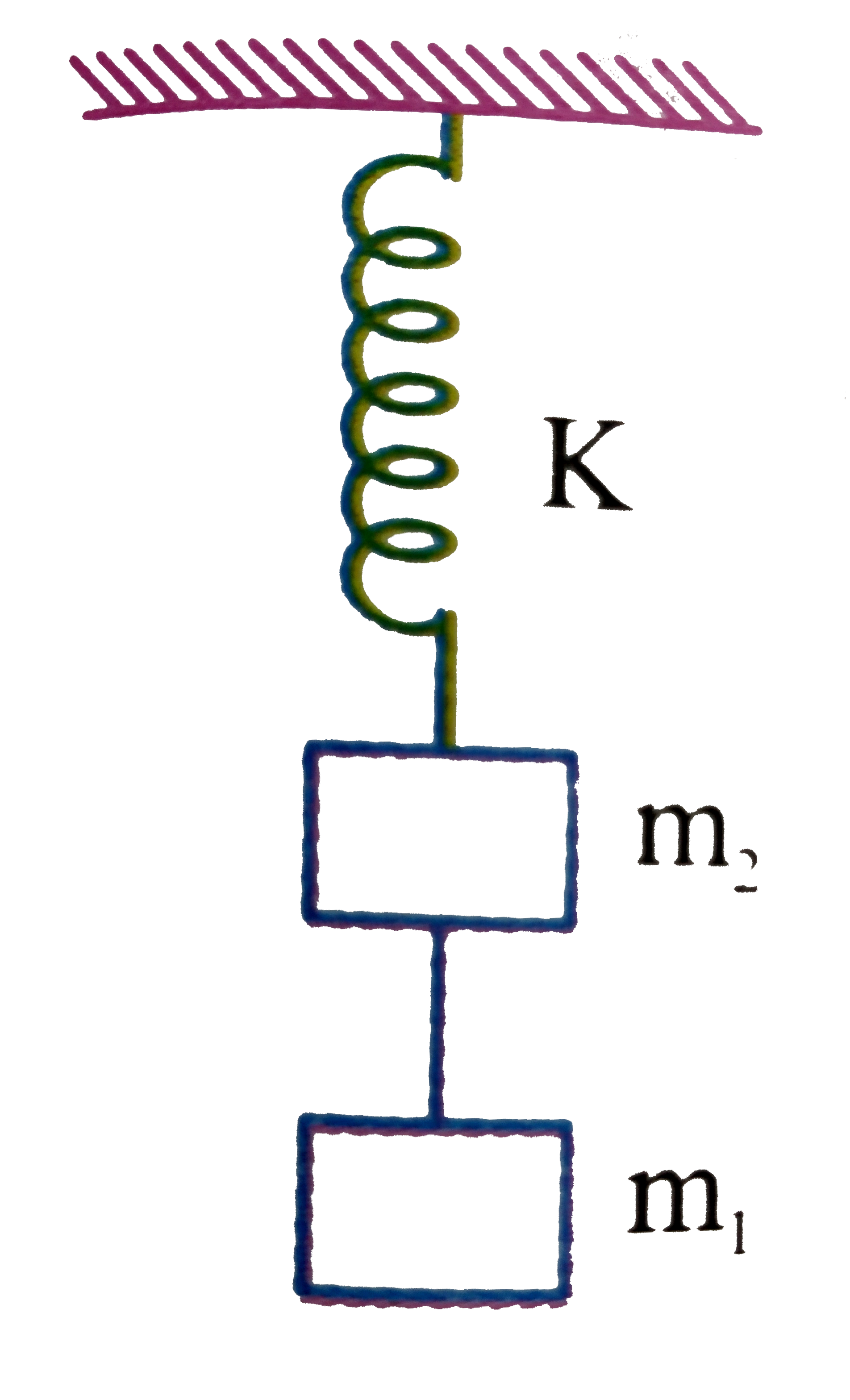 Aω=√Km1,Am2gKBω=√Km2,Am1gKCω=√Km1,A=m1gKDω=√Km1,A=m2gK
Aω=√Km1,Am2gKBω=√Km2,Am1gKCω=√Km1,A=m1gKDω=√Km1,A=m2gKTwo masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is
 Am1gKBm2gKC(m1+m2)gKD(m1−m2)gK
Am1gKBm2gKC(m1+m2)gKD(m1−m2)gKTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
AMgkBmgkC(M+m)gkD(M−m)gk
Two masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo masses m1=1.0kgandm2=0.5kg are suspended together by a massless spring of force constant, k=12.5Nm−1. When they are in equillibrium position, m1 is gently removed. Calculate the angular frequency and the amplitude of oscillation of m2. Given g=10ms−2.
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
View SolutionTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system. The amplitude of oscillation is
View Solution