The time period of a simple harmonic motion is 8 s At t=0. it is at the mean position.The ratio of the distance travelled bi it in the first and second seconds is,
12
1√2
√2
√2+1
The correct Answer is:D
Distance travelled in I second y1=Asin(2π8×1)=A√2
distance travelled in 2 seconds = A
distance travelled in 2nd second y2=A−A√2,
y1y2=A√2A−A√2=√2+1
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - I (H.W)
66 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (C.W)
27 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C. U . Q
75 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
The period of a particle in SHM is 8s. At t=0 it is in its equilibrium position.
(a) Compare the distance travelled in the first 4s and the second 4s.
(b) Compare the distance travelled in the first 2s and the second 2s.
View SolutionA particle executes SHM with time period 8 s. Initially, it is at its mean position. The ratio of distance travelled by it in the 1st second to that in the 2nd second is
View Solution
Knowledge Check
Time period of a particle executing SHM is 8 sec. At t=0 it is at the mean position. The ratio of the distance covered by the particle in the 1st second to the 2nd second is:
A1√2+1B√2C1√2D√2+1Time period of a particle executing SHM is 8 sec. At t=0 it is at the mean position. The ratio of the distance covered by the particle in the 1st second to the 2nd second is:
A1√2+1B√2C1√2D√2+1A particle oscillates simple harmonically along a straight line with period 8 seconds and amplitude 8√2m. It starts from the mean position, then the ratio of the distances travelled by it in the second second and first second of its motion is
A√2B2C(√2−1)D√3
The v-t graph for a particle is as shown. The distance travelled in the first seconds is :
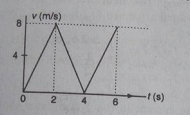
View SolutionThe v-t graph for a particle is as shown. The distance travelled in the first seconds is :

View SolutionThe v−t graph for a particle is shown. The distance travelled in the first four seconds is:

View SolutionA particle executes SHM with a time period of 8 s. It is starts from the extreme position at time t = 0, the ratio of distances covered by it in 1st and 2nd seconds is
View SolutionA body is executing a linear simple harmonic motion. At t=0, it is at one of the extreme position and travels 3cm in the first second and 4cm in the next second moving towards the other extreme position .
The amplitude of this S.H.M is
View Solution
